II. Charges in Motion Part 1
Simple Circuits, Voltage and Capacitance
Simple Circuits, Voltage and Capacitance
Video #3
In this third video of physics review for PEMF basic science, we are going to explore the energetics of voltage and capacitance and even see how it relates to the biophysics of the human cell. Then we will put charges into motion and leave electrostatics and enter the full glory of electrodynamics by first looking at very simple circuit ideas, MAINLY current (which IS charges in motion). First let's review a little.
In the last video we saw that charge is a fundamental property which gives rise to the electromagnetic force just as mass gives rise to the gravitational force.
There are two types of electric charges; positive and negative (commonly carried by protons and electrons respectively). Like charges repel and unlike attract.
Coulombs law told us the electric force between two or more charges, but we found it is easier and more powerful to use the field formulation, as it defines the electric field at ALL points in space. Electric field FLOWS out of positive charges and INTO negative charges. The density of the field lines corresponds to the strength of the field. And it is the field that exerts or transmits the electric force, not some action at a distance.
In this third video of physics review for PEMF basic science, we are going to explore the energetics of voltage and capacitance and even see how it relates to the biophysics of the human cell. Then we will put charges into motion and leave electrostatics and enter the full glory of electrodynamics by first looking at very simple circuit ideas, MAINLY current (which IS charges in motion). First let's review a little.
In the last video we saw that charge is a fundamental property which gives rise to the electromagnetic force just as mass gives rise to the gravitational force.
There are two types of electric charges; positive and negative (commonly carried by protons and electrons respectively). Like charges repel and unlike attract.
Coulombs law told us the electric force between two or more charges, but we found it is easier and more powerful to use the field formulation, as it defines the electric field at ALL points in space. Electric field FLOWS out of positive charges and INTO negative charges. The density of the field lines corresponds to the strength of the field. And it is the field that exerts or transmits the electric force, not some action at a distance.
In Electric Charge and Electric Field, we just scratched the surface (or at least rubbed it) of electrical phenomena. Two of the most familiar aspects of electricity are its energy and voltage. We know, for example, that great amounts of electrical energy can be stored in batteries, are transmitted cross-country through power lines, and may jump from clouds to explode the sap of trees. In a similar manner, at molecular levels, ions cross cell membranes and transfer information. We also know about voltages associated with electricity. Batteries are typically a few volts, the outlets in your home produce 120 volts, and power lines can be as high as hundreds of thousands of volts. But energy and voltage are not the same thing.
A motorcycle battery, for example, is small and would not be very successful in replacing the much larger car battery, yet each has the same voltage. In this chapter, we shall examine the relationship between voltage and electrical energy and begin to explore some of the many applications of electricity.
A motorcycle battery, for example, is small and would not be very successful in replacing the much larger car battery, yet each has the same voltage. In this chapter, we shall examine the relationship between voltage and electrical energy and begin to explore some of the many applications of electricity.
But lets begin by looking at the idea of voltage in terms of stationary charges which are able to store (potential) energy. But since Voltage is defined as the work done per unit charge, let's review the idea of work.
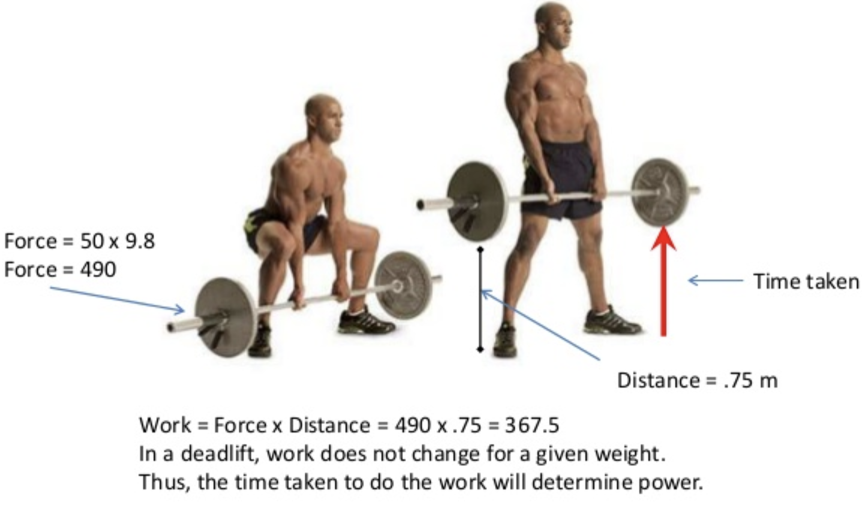
Work is a measure of energy in physics and equals Force x Distance. When you work out, you really ARE doing work in the physics sense of the word. So when you left a 50 kilogram weight a distance of .75 meters. F = ma so the force is 50kg x 9.8m/s^2 which is a force of 490 Newtons. The work done is force x distance = 490 x .75 meters = 367.5 Joules. You know from experience that takes ENERGY to lift a weight and the amount of energy is force times distance. Here the work is being done against the gravitational field. As we'll see now, Voltage is the work down against an electric field.
And remember the Units for Energy are Joules (calories are also units for energy as you can relate energy stored in food). So Joules and Calories are like Kilometers and Miles, different units to describe the same property (Energy).
Work is a measure of energy in physics and equals Force x Distance. When you work out, you really ARE doing work in the physics sense of the word. So when you left a 50 kilogram weight a distance of .75 meters. F = ma so the force is 50kg x 9.8m/s^2 which is a force of 490 Newtons. The work done is force x distance = 490 x .75 meters = 367.5 Joules. You know from experience that takes ENERGY to lift a weight and the amount of energy is force times distance. Here the work is being done against the gravitational field. As we'll see now, Voltage is the work down against an electric field.
And remember the Units for Energy are Joules (calories are also units for energy as you can relate energy stored in food). So Joules and Calories are like Kilometers and Miles, different units to describe the same property (Energy).
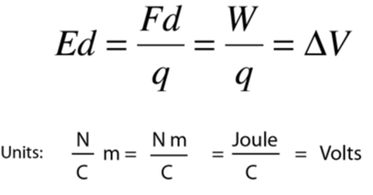
Voltage (or Electrical Potential)
The electrical potential (Voltage) is defined as the work required to move one Coulomb of charge by one meter. The units of Volts are Joules/Coulomb which is energy per unit charge.
That is, it takes ENERGY to pull apart two oppositely charged particles because they want to stick together, just like two magnets. Think how you have to really "work" to separate two strong magnets. Similarly it takes work to push together two similarly charged particles (think of pushing two north poles together.
The electrical potential (Voltage) is defined as the work required to move one Coulomb of charge by one meter. The units of Volts are Joules/Coulomb which is energy per unit charge.
That is, it takes ENERGY to pull apart two oppositely charged particles because they want to stick together, just like two magnets. Think how you have to really "work" to separate two strong magnets. Similarly it takes work to push together two similarly charged particles (think of pushing two north poles together.
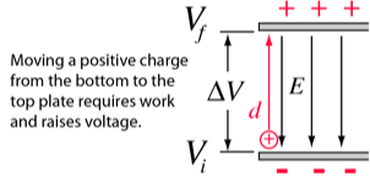
So instead of moving weight against a gravitation Field like our previous example of work, we are moving charge against an electric field. Remember the electric field flows out of a positive charge and into a negative charge, so if we "push" or "move" a positive charge upstream to more positive charges, it is like rowing upstream, we need to supply energy or "work" to move it. Usually the goal of moving charges is to separate positive and negative charges so energy can be stored.
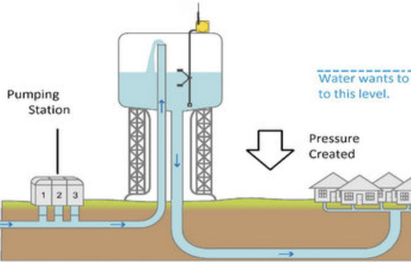
A water tower is a way to store gravitational potential energy. It takes work to pump the water up to the water tower, but once there, energy is stored such that water pressure (force per area) can be released at will. Voltage is very much like an electrical "pressure" analogous to water pressure.
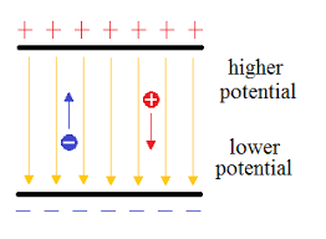
NOTE:
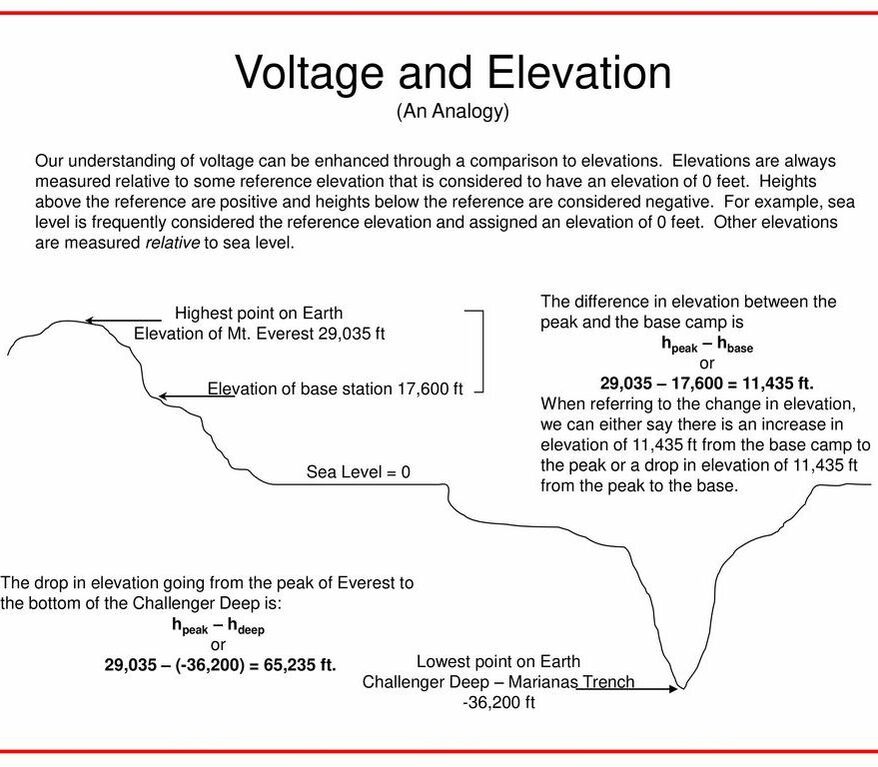
Keep in mind that whenever a voltage is quoted, it is understood to be the potential difference between two points. For example, every battery has two terminals, and its voltage is the potential difference between them. More fundamentally, the point you choose to be zero volts is arbitrary. This is analogous to the fact that gravitational potential energy has an arbitrary zero, such as sea level.
So voltage is kinda like elevation, it is the difference between two levels and the reference point needs to be set (which we usually set at sea level).
Keep in mind that whenever a voltage is quoted, it is understood to be the potential difference between two points. For example, every battery has two terminals, and its voltage is the potential difference between them. More fundamentally, the point you choose to be zero volts is arbitrary. This is analogous to the fact that gravitational potential energy has an arbitrary zero, such as sea level.
So voltage is kinda like elevation, it is the difference between two levels and the reference point needs to be set (which we usually set at sea level).
IMPORTANT NOTE***: Voltage is not the same as energy. Voltage is the energy per unit charge. Thus a motorcycle battery and a car battery can both have the same voltage (more precisely, the same potential difference between battery terminals), yet one stores much more energy than the other since ΔPE = qΔV. The car battery can move more charge than the motorcycle battery, although both are 12 V batteries.
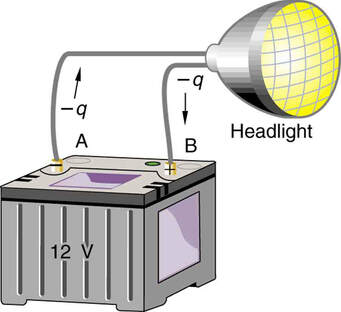
ASIDE #1 Voltage and Batteries:
A battery moves negative charge from its negative terminal through a headlight to its positive terminal. Appropriate combinations of chemicals in the battery separate charges so that the negative terminal has an excess of negative charge, which is repelled by it and attracted to the excess positive charge on the other terminal.
In terms of potential, the positive terminal is at a higher voltage than the negative. Inside the battery, both positive and negative charges move.
The voltage of the battery is the DIFFERENCE between the positive and negative terminals.
A battery moves negative charge from its negative terminal through a headlight to its positive terminal. Appropriate combinations of chemicals in the battery separate charges so that the negative terminal has an excess of negative charge, which is repelled by it and attracted to the excess positive charge on the other terminal.
In terms of potential, the positive terminal is at a higher voltage than the negative. Inside the battery, both positive and negative charges move.
The voltage of the battery is the DIFFERENCE between the positive and negative terminals.
ASIDE #2: Voltage AND PEMF
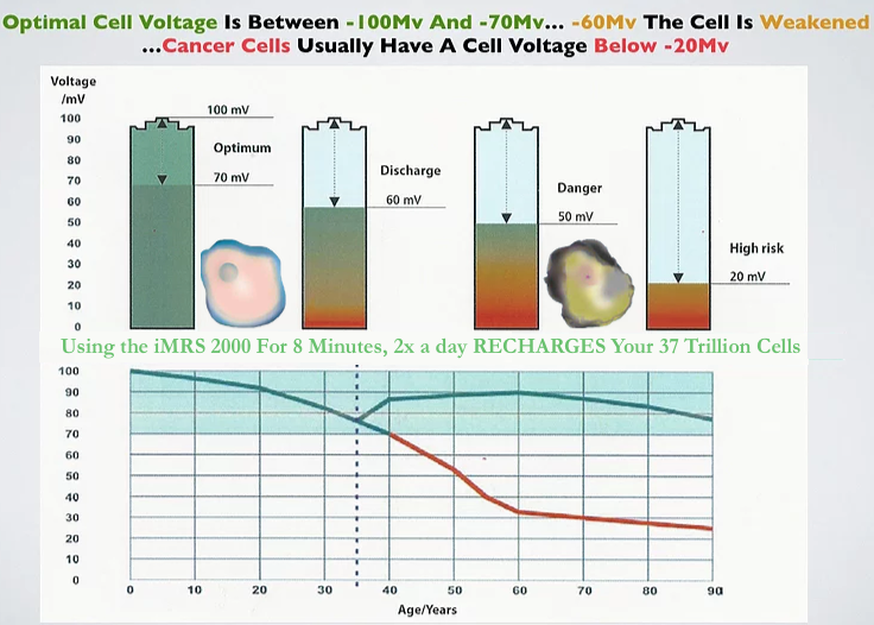
Almost all chronic diseases are characterized by low voltage, that is low cellular energy.
Voltage is stored across the cell membrane of every cell to give cells energy to work. This is due to the cells have a net positive charge on the outside of the cell and a net negative charge on the inside. Depending on how you choose your zero, you can get different values but the resting potential across the cell membrane is generally accepted to be -70 millivolts.
Almost all chronic diseases are characterized by low voltage, that is low cellular energy.
Voltage is stored across the cell membrane of every cell to give cells energy to work. This is due to the cells have a net positive charge on the outside of the cell and a net negative charge on the inside. Depending on how you choose your zero, you can get different values but the resting potential across the cell membrane is generally accepted to be -70 millivolts.
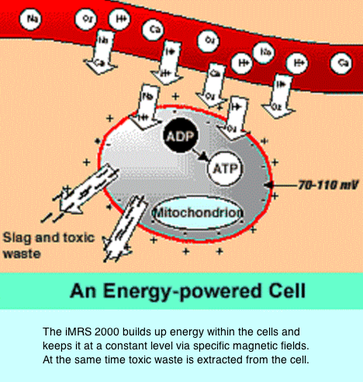
So how does PEMF recharge the voltage of your cells and increase TMP.
As you sweep magnetic fields back and forth across the cell membrane at the proper resonant frequencies (0-50 Hz), they generate a whole lot of activity in the cell via resonant energy transfer.
Then MAIN effect is the benefits on the Trans Membrane Potential (or Voltage) and its associated ion pumps, the main ones being Sodium/Potassium and Calcium/Magnesium pumps. The main effect of PEMF is to open these channels favorably and create charge separation which increases VOLTAGE which INCREASES CELLULAR ENERGY!!
As you sweep magnetic fields back and forth across the cell membrane at the proper resonant frequencies (0-50 Hz), they generate a whole lot of activity in the cell via resonant energy transfer.
Then MAIN effect is the benefits on the Trans Membrane Potential (or Voltage) and its associated ion pumps, the main ones being Sodium/Potassium and Calcium/Magnesium pumps. The main effect of PEMF is to open these channels favorably and create charge separation which increases VOLTAGE which INCREASES CELLULAR ENERGY!!
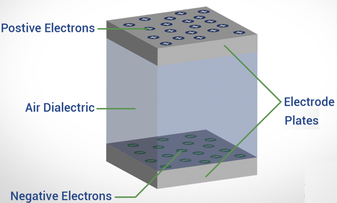
Ok, so once we Move Charges Apart, How to we keep them separated?? The answer is via a capacitor of some sort. A capacitor is a device that can hold or store separated charges much like a water tower stores energy by elevating or separating water from the ground.
A capacitor consists of two conducting plates separated by an insulating layer called a dielectric (more on dielectrics later).
A capacitor consists of two conducting plates separated by an insulating layer called a dielectric (more on dielectrics later).
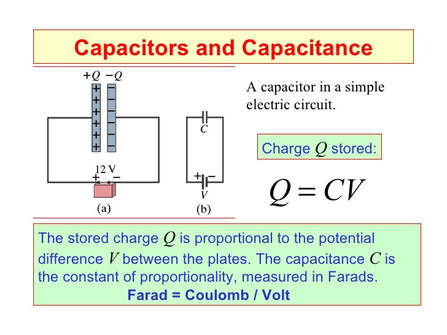
The Stored charge is proportional to the Potential Difference (or Voltage) between the plates. The constant of proportionality is called the capacitance measured in Farads (C = Q/V or Coulombs per Volt).
NOTE: capacitors in most consumer-level devices deal with thousandths of a farad (microfarads, µF) or smaller.
NOTE: capacitors in most consumer-level devices deal with thousandths of a farad (microfarads, µF) or smaller.
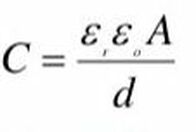
Capacitors with an air dielectric (that is air in between), have a capacitance equal to the Area of plates divided by the distance in between. C is a geometric quantity in that it is an Area divided by a distance (as we'll see the same is true with inductance). So Larger plates closer together will have greater capacitance than small plates father away.
Another interesting biological example dealing with electric potential is found in the cell’s plasma membrane. The membrane sets a cell off from its surroundings and also allows ions to selectively pass in and out of the cell. There is a potential difference across the membrane of about –70 mV . This is due to the mainly negatively charged ions in the cell and the predominance of positively charged sodium (Na+) ions outside.
Things change when a nerve cell is stimulated. Na+ ions are allowed to pass through the membrane into the cell, producing a positive membrane potential—the nerve signal.
Things change when a nerve cell is stimulated. Na+ ions are allowed to pass through the membrane into the cell, producing a positive membrane potential—the nerve signal.
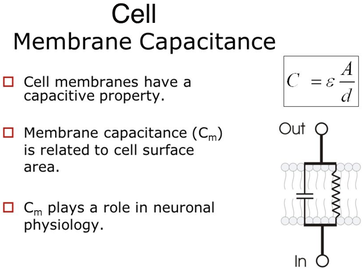
The cell membrane of each of your 37 trillion cells acts as a capacitor that can keep charges separated until the energy is needed. This is how the cellular voltage is stored.
The inside and the outside of the cell are both solutions of various salts in water. As opposed to the cell membrane, salt water constitutes quite a good conductor because there are free ions that can transport electrical charges.
What we have then is two conductors (the inside and the outside of the cell), separated by an insulator (the membrane). This makes it possible to have different amounts of electrical charges inside and outside the cell. If we can separate a charge Q by applying an electrical potential V across the membrane, the membrane has by definition a capacitance C=Q/V .
In fact, because the membrane is so thin (only two molecules thick, with a total thickness of about 7×10−9m), we don't need much voltage to separate the charges and therefore the membrane capacitance is quite high; per unit area, it is
c=CS≈10−2Fm−2(1)... Which is 10 millifarads / meter squared... That is an enormous capacitance as most industrial capacitors are in the micro farad range. As we mentioned, F is the SI unit of capacitance ("Farad").
To put this in perspective, the electric field across the cell membrane = V/d (Voltage divided by distance) which is .070 volts/7x10^-9meters = 10,000,000 volts per meter!! That is an incredible amount of energy considering how small cells are.
The inside and the outside of the cell are both solutions of various salts in water. As opposed to the cell membrane, salt water constitutes quite a good conductor because there are free ions that can transport electrical charges.
What we have then is two conductors (the inside and the outside of the cell), separated by an insulator (the membrane). This makes it possible to have different amounts of electrical charges inside and outside the cell. If we can separate a charge Q by applying an electrical potential V across the membrane, the membrane has by definition a capacitance C=Q/V .
In fact, because the membrane is so thin (only two molecules thick, with a total thickness of about 7×10−9m), we don't need much voltage to separate the charges and therefore the membrane capacitance is quite high; per unit area, it is
c=CS≈10−2Fm−2(1)... Which is 10 millifarads / meter squared... That is an enormous capacitance as most industrial capacitors are in the micro farad range. As we mentioned, F is the SI unit of capacitance ("Farad").
To put this in perspective, the electric field across the cell membrane = V/d (Voltage divided by distance) which is .070 volts/7x10^-9meters = 10,000,000 volts per meter!! That is an incredible amount of energy considering how small cells are.
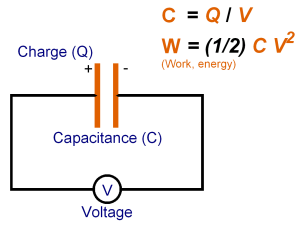
So You can also think of a capacitor (like the cell membrane) as a device that stores Energy BECAUSE it keeps the positive and negative charges separated (like a water tower stores energy).
So it always takes energy of some force to separate charge, but once separated, across an insulator (like air), there is energy stored that can do work when needed. I won't derive it but the energy stored is equal to the Work required to separate the Charges = 1/2 CV^2.
So it takes WORK to separate charge in a capacitor and once separated the capacitor stores energy.
Again think of a water tower, the energy spent to pump the water up the tower is going to be roughly equal (minus heat loss) to the energy stored).
In the case of the human cell, work is usually provided by ATP to separate charge (namely pushing 3 Na out and 2 K in), BUT PEMF can help to DIRECTLY move charges because a changing magnetic field induces an electric current, AS WE'LL see in the section on Faradays law.
PEMF can act as a FORCE to separate to help separate charges in the body which overall increases the body's and cells amount of stored energy. Otherwise the body needs to use precious ATP to separate charges.
Separating Charge is ONE OF THE KEYS to energizing not only electronics, but life itself! IN fact the more I study biophysics, it just may be THE key to life, especially in the efficiency that life is able to separate charges.
As we just saw, to keep the charges separated you need an insulator, so lets look briefly at what a conductor and insulator is as you probably already know. Let's start with conductors.
(there are also semiconductors, but we'll save that for another course on quantum mechanics and quantum biology).
So it always takes energy of some force to separate charge, but once separated, across an insulator (like air), there is energy stored that can do work when needed. I won't derive it but the energy stored is equal to the Work required to separate the Charges = 1/2 CV^2.
So it takes WORK to separate charge in a capacitor and once separated the capacitor stores energy.
Again think of a water tower, the energy spent to pump the water up the tower is going to be roughly equal (minus heat loss) to the energy stored).
In the case of the human cell, work is usually provided by ATP to separate charge (namely pushing 3 Na out and 2 K in), BUT PEMF can help to DIRECTLY move charges because a changing magnetic field induces an electric current, AS WE'LL see in the section on Faradays law.
PEMF can act as a FORCE to separate to help separate charges in the body which overall increases the body's and cells amount of stored energy. Otherwise the body needs to use precious ATP to separate charges.
Separating Charge is ONE OF THE KEYS to energizing not only electronics, but life itself! IN fact the more I study biophysics, it just may be THE key to life, especially in the efficiency that life is able to separate charges.
As we just saw, to keep the charges separated you need an insulator, so lets look briefly at what a conductor and insulator is as you probably already know. Let's start with conductors.
(there are also semiconductors, but we'll save that for another course on quantum mechanics and quantum biology).
Conductors and Insulators
Some substances, such as metals (especially copper, silver, gold and aluminum) and salty water, allow charges to move through them with relative ease. Some of the electrons in metals and similar conductors are not bound to individual atoms or sites in the material.
Any substance that has free electrons and allows charge to move relatively freely through it is called a conductor.
Salty water and other similar conducting materials contain free ions that can move through them. An ion is an atom or molecule having a positive or negative (nonzero) total charge and acts as the charge carrier in ionic solutions like salt water and human plasma, just as electrons are the charge carriers in metals.
This form of conduction is important in the human body, where the main ion charge carriers are Ca+, Na+, K+, Cl-. But the body also uses H+, and electrons to transport energy and charge, so PEMF is working on the human body to MOVE charge which INCREASES stored (TMP/ATP) and kinetic energy (Nerve/Meridian/Blood flow).
Any substance that has free electrons and allows charge to move relatively freely through it is called a conductor.
Salty water and other similar conducting materials contain free ions that can move through them. An ion is an atom or molecule having a positive or negative (nonzero) total charge and acts as the charge carrier in ionic solutions like salt water and human plasma, just as electrons are the charge carriers in metals.
This form of conduction is important in the human body, where the main ion charge carriers are Ca+, Na+, K+, Cl-. But the body also uses H+, and electrons to transport energy and charge, so PEMF is working on the human body to MOVE charge which INCREASES stored (TMP/ATP) and kinetic energy (Nerve/Meridian/Blood flow).
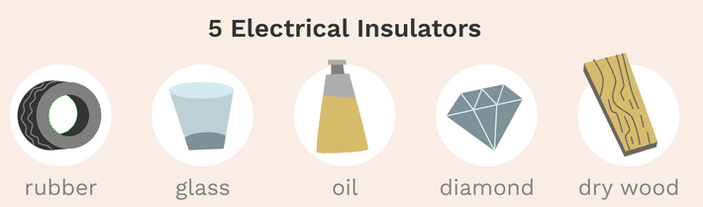
Materials such as glass, fabric, plastic and rubber that do not allow free flow of charge are called insulators. Electrons and ions in insulators are bound in the structure and cannot move easily—as much as 10^23 times more slowly than in conductors.
In the case of rubber soles on shoes it is a BAD thing that our shoes are insulators. We WANT the flow of electrons from the earth to move into our feet and body. Barefoot and natural leather and certain shoes on the market (grounders, etc.) conduct these healing earthing electrons.
In the case of rubber soles on shoes it is a BAD thing that our shoes are insulators. We WANT the flow of electrons from the earth to move into our feet and body. Barefoot and natural leather and certain shoes on the market (grounders, etc.) conduct these healing earthing electrons.

This power adapter like used in PEMF devices uses metal wires and connectors to conduct electricity from the wall socket to a laptop computer. The conducting wires allow electrons to move freely through the cables, which are shielded by rubber and plastic. These materials act as insulators that don’t allow electric charge to escape outward.

The moving electrons may collide with fixed atoms and molecules, losing some energy, but they can move in a conductor. This is called resistance (more on this later).
Superconductors allow the movement of charge without any loss of energy which means ZERO resistance.
The goal of human health is to LOWER the resistance to energy flows in the nerves, blood, lymph and meridian systems. The more we can be like a superconductor, the younger and healthier we will be. PEMF helps by OPENING all these fractal and flowing networks.
Note: superconductors are free from impurities and as such are perfect crystalline networks. There is good evidence the human body is a liquid crystal with superconducting potential if we can keep it clean and free of impurities and blockages.
Superconductors allow the movement of charge without any loss of energy which means ZERO resistance.
The goal of human health is to LOWER the resistance to energy flows in the nerves, blood, lymph and meridian systems. The more we can be like a superconductor, the younger and healthier we will be. PEMF helps by OPENING all these fractal and flowing networks.
Note: superconductors are free from impurities and as such are perfect crystalline networks. There is good evidence the human body is a liquid crystal with superconducting potential if we can keep it clean and free of impurities and blockages.
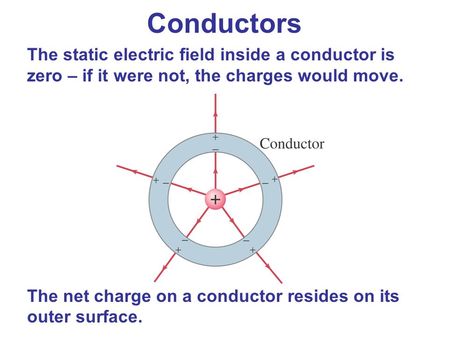
Conductors
Contain an unlimited supply of charges that are free to move about through the material. This means that many of the electrons (one or two per atom in a typical metal) are not associated with any particular nucleus, but FREE to roam around at will.
NOTE: Electric Fields in Conductors are Zero because the free charges all balance out to create an opposing electric field.
Negative Charges migrate to cancel the field because they are attracted to positive charges.
Charges remain on surface UNLESS a strong field, then you can have corona discharge (lightning). This is St Elmos Fire.
Contain an unlimited supply of charges that are free to move about through the material. This means that many of the electrons (one or two per atom in a typical metal) are not associated with any particular nucleus, but FREE to roam around at will.
NOTE: Electric Fields in Conductors are Zero because the free charges all balance out to create an opposing electric field.
Negative Charges migrate to cancel the field because they are attracted to positive charges.
Charges remain on surface UNLESS a strong field, then you can have corona discharge (lightning). This is St Elmos Fire.
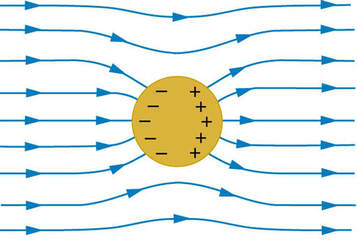
A conductor placed in an electric field will be polarized. This Figure shows the result of placing a neutral conductor in an originally uniform electric field. The field becomes stronger near the conductor but entirely disappears inside it.
Free charges move within the conductor, polarizing it, until the electric field lines are perpendicular to the surface.
The field lines end on excess negative charge on one section of the surface and begin again on excess positive charge on the opposite side.
No electric field exists inside the conductor, since free charges in the conductor would continue moving in response to any field until it was neutralized.
Free charges move within the conductor, polarizing it, until the electric field lines are perpendicular to the surface.
The field lines end on excess negative charge on one section of the surface and begin again on excess positive charge on the opposite side.
No electric field exists inside the conductor, since free charges in the conductor would continue moving in response to any field until it was neutralized.

Insulators by contrast are materials that DO NOT allow charges to easily flow. That is the electrons are on a tight lease, and all they can do is move a bit within the atom of molecule.
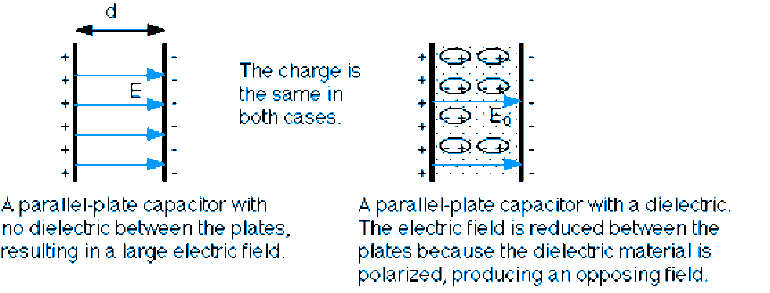
When a substance is filled with a Insulator which we will now refer to as a dielectric, the electric field everywhere is reduced by a factor of 1 over what is called the dielectric constant.
Coulombs law stays the same in insulators or dielectrics, you just divide by the dielectric constant.
The dielectric constant is factor indicating, how much the interaction force between two charges will be diminished, if not vacuum, but a real substance is in between.
The larger the dielectric, the greater the shielding or reduction of the electric field in the material. The greater the dielectric constant.
Because of that they do NOT conduct electricity (or heat) very well. So they cannot cancel out the electric field like a metal, BUT the molecules in a dielectric become what is called polarized because they CAN MOVE A LITTLE. And it is this polarization that shields the charges.
When a substance is filled with a Insulator which we will now refer to as a dielectric, the electric field everywhere is reduced by a factor of 1 over what is called the dielectric constant.
Coulombs law stays the same in insulators or dielectrics, you just divide by the dielectric constant.
The dielectric constant is factor indicating, how much the interaction force between two charges will be diminished, if not vacuum, but a real substance is in between.
The larger the dielectric, the greater the shielding or reduction of the electric field in the material. The greater the dielectric constant.
Because of that they do NOT conduct electricity (or heat) very well. So they cannot cancel out the electric field like a metal, BUT the molecules in a dielectric become what is called polarized because they CAN MOVE A LITTLE. And it is this polarization that shields the charges.
So The dielectric constant is a measure of how much the electric field is blocked or shielded in a given material. So for free space the dielectric constant is 1 (which leaves Coulombs law unchanged) and for conductors, the dielectric is infinite (because the electric field is zero), but most materials are somewhere in between.
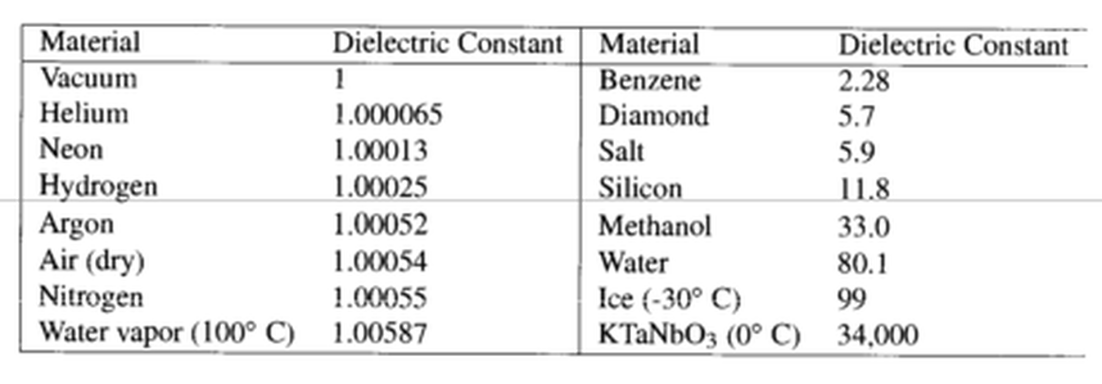
Here are a few examples of dielectrics in different materials.
Here are a few examples of dielectrics in different materials.
NOTE: Coulombs law is for and air is very close to 1, so the answers still work out in a laboratory and classrooms with experiments that demonstrate Coulombs law. I know this because I did such lab experiments when I taught physics with Pith balls. You can use Coulombs law to determine how much charge is on two pith balls by measuring the distance the balls separate.
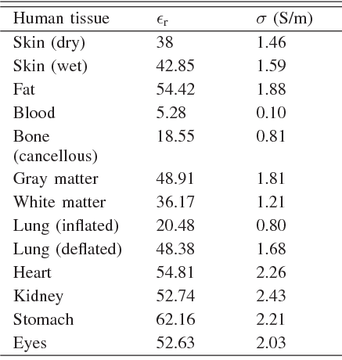
Unlike air, Water on the other hand would shield the electric force by 80 fold (divide by 80 - sea water is around 88). So the human body which is mostly water w/ electrolytes is NOT at all transparent to Electric fields (unlike magnetic fields which go right through).
You can see here some of the dielectric constants of the human body. Notice that ALL tissues in the body shield the electric field significantly!
This is why magnetic field therapy is better than electric currents and electric fields, because (as we'll see) if goes through with no shielding and no reduction!!!
NOTE 2: Dielectric Constant is sometimes called relative permittivity which might be a better terminology because dielectrics DO change with frequency (so far we are only dealing with electrostatics). For example the dielectric of ice changes from approx 81 at frequencies below 1 kHz to less than 5 at frequencies above 1 MHz.
Since most GOOD PEMF devices use LOW frequency ELF, this is not a big factor (but it certainly IS WITH 4G and 5G signals... Lower Dielectric means LESS shielding which in this case is BAD!!!
You can see here some of the dielectric constants of the human body. Notice that ALL tissues in the body shield the electric field significantly!
This is why magnetic field therapy is better than electric currents and electric fields, because (as we'll see) if goes through with no shielding and no reduction!!!
NOTE 2: Dielectric Constant is sometimes called relative permittivity which might be a better terminology because dielectrics DO change with frequency (so far we are only dealing with electrostatics). For example the dielectric of ice changes from approx 81 at frequencies below 1 kHz to less than 5 at frequencies above 1 MHz.
Since most GOOD PEMF devices use LOW frequency ELF, this is not a big factor (but it certainly IS WITH 4G and 5G signals... Lower Dielectric means LESS shielding which in this case is BAD!!!
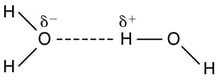
ASIDE: Dielectrics and Screening the Coulomb Force in the Human Body.
One might wonder why electrostatic forces do not play a larger role in biology than they do if we have so many charged molecules. The reason is that the electrostatic force is “diluted” due to screening between molecules. This is due to the presence of other charges in the cell.
The best example of this charge screening is the water molecule, represented as H2O. Water is a strongly polar molecule. Its 10 electrons (8 from the oxygen atom and 2 from the two hydrogen atoms) tend to remain closer to the oxygen nucleus than the hydrogen nuclei. This creates two centers of equal and opposite charges—what is called a dipole, as illustrated in this Figure.
The symbols δ− and δ+ indicate that the oxygen side of the H2O molecule tends to be more negative, while the hydrogen ends tend to be more positive. This leads to an attraction of opposite charges between molecules.
These two centers of charge will terminate some of the electric field lines coming from a free charge, as on a DNA molecule. This results in a reduction in the strength of the Coulomb interaction. One might say that screening makes the Coulomb force a short range force rather than long range.
Other ions of importance in biology that can reduce or screen Coulomb interactions are Na+, and K+, and Cl–. These ions are located both inside and outside of living cells. The movement of these ions through cell membranes is crucial to the motion of nerve impulses through nerve axons.
One might wonder why electrostatic forces do not play a larger role in biology than they do if we have so many charged molecules. The reason is that the electrostatic force is “diluted” due to screening between molecules. This is due to the presence of other charges in the cell.
The best example of this charge screening is the water molecule, represented as H2O. Water is a strongly polar molecule. Its 10 electrons (8 from the oxygen atom and 2 from the two hydrogen atoms) tend to remain closer to the oxygen nucleus than the hydrogen nuclei. This creates two centers of equal and opposite charges—what is called a dipole, as illustrated in this Figure.
The symbols δ− and δ+ indicate that the oxygen side of the H2O molecule tends to be more negative, while the hydrogen ends tend to be more positive. This leads to an attraction of opposite charges between molecules.
These two centers of charge will terminate some of the electric field lines coming from a free charge, as on a DNA molecule. This results in a reduction in the strength of the Coulomb interaction. One might say that screening makes the Coulomb force a short range force rather than long range.
Other ions of importance in biology that can reduce or screen Coulomb interactions are Na+, and K+, and Cl–. These ions are located both inside and outside of living cells. The movement of these ions through cell membranes is crucial to the motion of nerve impulses through nerve axons.

Capacitors Revisited
A capacitor consists of two conducting plates separated by an insulating layer or dielectric.
Capacitors Require a LARGE dielectric or strong insulator to reduce electric field between the plates and effectively keep the charges separated.
Otherwise charges would just flow from one side to the other via corona discharge due to the large electric field OR conductive across is the material is conducting.
This is why you want to use a dielectric ALONG with a large surface area and small distance. And because a small distance between the plates INCREASES the capacitance, you need something to BLOCK the charges from just jumping across. And this is why you use a dielectric (or insulator) why a large dielectric constant, because it will effectively keep the charges separated.
C = eA/d (to increase capacitance, increase Surface area, increase dielectric and decrease distance between plates.
The cell membrane is a VERY strong insulator except in the selective ion channels. The dielectric of the cell membrane er is around 5 (reduces electric field to 1/5 = 20%), giving rise to a capacitance of 10–2 F/m2. From an electrical viewpoint, the lipid bilayer portion of the membrane is a good insulator which makes for a good capacitor.
ASIDE:
Interestingly supercapacitors work to increase A = surface area which is why there is recent interest in employing graphene in supercapacitors, as graphene is arguably
the ‘ultimate’ material for creation of high surface area electrodes (capacitor plates).
The biggest improvement resulted from new techniques that permit the fabrication of thinner ceramic dielectric layers. Enhancements in the dielectric constant of the best ceramic have been more modest. In fact, most of the effort to increase dielectric constant has focused on improving one material, barium titanate, for decades (5-9).
Barium titanate is a dielectric ceramic used in capacitors, with dielectric constant values as high as 7,000. Over a narrow temperature range, values as high as 15,000 are possible; most common ceramic and polymer materials are less than 10.
A capacitor consists of two conducting plates separated by an insulating layer or dielectric.
Capacitors Require a LARGE dielectric or strong insulator to reduce electric field between the plates and effectively keep the charges separated.
Otherwise charges would just flow from one side to the other via corona discharge due to the large electric field OR conductive across is the material is conducting.
This is why you want to use a dielectric ALONG with a large surface area and small distance. And because a small distance between the plates INCREASES the capacitance, you need something to BLOCK the charges from just jumping across. And this is why you use a dielectric (or insulator) why a large dielectric constant, because it will effectively keep the charges separated.
C = eA/d (to increase capacitance, increase Surface area, increase dielectric and decrease distance between plates.
The cell membrane is a VERY strong insulator except in the selective ion channels. The dielectric of the cell membrane er is around 5 (reduces electric field to 1/5 = 20%), giving rise to a capacitance of 10–2 F/m2. From an electrical viewpoint, the lipid bilayer portion of the membrane is a good insulator which makes for a good capacitor.
ASIDE:
Interestingly supercapacitors work to increase A = surface area which is why there is recent interest in employing graphene in supercapacitors, as graphene is arguably
the ‘ultimate’ material for creation of high surface area electrodes (capacitor plates).
The biggest improvement resulted from new techniques that permit the fabrication of thinner ceramic dielectric layers. Enhancements in the dielectric constant of the best ceramic have been more modest. In fact, most of the effort to increase dielectric constant has focused on improving one material, barium titanate, for decades (5-9).
Barium titanate is a dielectric ceramic used in capacitors, with dielectric constant values as high as 7,000. Over a narrow temperature range, values as high as 15,000 are possible; most common ceramic and polymer materials are less than 10.
II. Charges in Motion Part 1 (Basics D.C. Circuits).
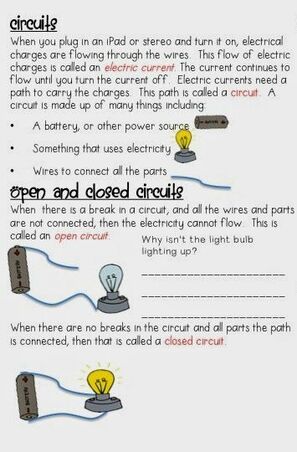
Electric circuits are commonplace. Some are simple, such as those in flashlights. Others, such as those used in supercomputers, are extremely complex. In this module, we'll start with D.C. simple circuits and introduce Ohms Law.
D.C. circuits are circuits that have steady currents that DO NOT change with time. That is they are static currents with no frequency. PEMF devices most definitely have time varying currents, but A.C. circuit theory is much more complex, and you can many times you can use quasistatic approximations for PEMF fields because they are HOPEFULLY low frequency, earth based devices. (I am very much against high frequency PEMF, because it is unnatural and effectively electrosmog).With Most PEMF Devices the circuit basically consists of 3 things...
1) the source of electricity is a wall socket which receives electricity from the power company or battery for cheaper and weaker systems.
2) Conducting wire (usually copper) of proper thickness to connect all the coils with the control until. More on the best wire later.
3) ...and what USES the electricity is
a. first the control unit which generates the time varying current (which as we'll see generates a time varying magnetic field or PEMF).
b. and then the circular CURRENT LOOPS in the PEMF device. This is where most of the power goes.
We are going to talk a lot more about this in this course, but let's just introduce these three main elements of basic D.C. circuits.
1) Current (I)
2) Resistance (R) or Conductance
3) Voltage (V) or EMF
Note Capacitance and Inductance are the other two main elements. We discussed capacitance a little already and we'll later look at inductance later on with Faraday's law as it deals more with time varying currents.
D.C. circuits are circuits that have steady currents that DO NOT change with time. That is they are static currents with no frequency. PEMF devices most definitely have time varying currents, but A.C. circuit theory is much more complex, and you can many times you can use quasistatic approximations for PEMF fields because they are HOPEFULLY low frequency, earth based devices. (I am very much against high frequency PEMF, because it is unnatural and effectively electrosmog).With Most PEMF Devices the circuit basically consists of 3 things...
1) the source of electricity is a wall socket which receives electricity from the power company or battery for cheaper and weaker systems.
2) Conducting wire (usually copper) of proper thickness to connect all the coils with the control until. More on the best wire later.
3) ...and what USES the electricity is
a. first the control unit which generates the time varying current (which as we'll see generates a time varying magnetic field or PEMF).
b. and then the circular CURRENT LOOPS in the PEMF device. This is where most of the power goes.
We are going to talk a lot more about this in this course, but let's just introduce these three main elements of basic D.C. circuits.
1) Current (I)
2) Resistance (R) or Conductance
3) Voltage (V) or EMF
Note Capacitance and Inductance are the other two main elements. We discussed capacitance a little already and we'll later look at inductance later on with Faraday's law as it deals more with time varying currents.
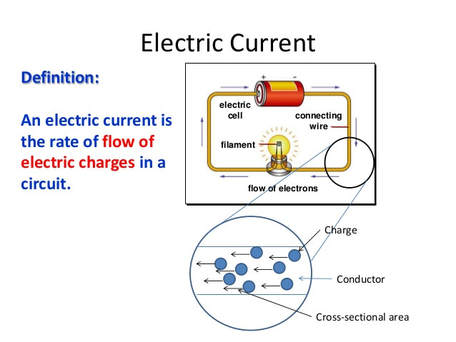
Current (I):
The first thing in electrical circuits is, you’ve got some wire and you’ve got an electric current flowing in it. We need a description of the current.
The current is defined as follows. Imagine the wire is a perfect cylinder, cross section A. You cut it somewhere and you watch all the charges go by, and you see the number of coulombs that go by per second. That’s called the electric current and is measured in amperes. So 1 coulomb per second is 1 amp.
So Electric Current is the rate of flow of an electric charge per unit time in a conducing wire.
The first thing in electrical circuits is, you’ve got some wire and you’ve got an electric current flowing in it. We need a description of the current.
The current is defined as follows. Imagine the wire is a perfect cylinder, cross section A. You cut it somewhere and you watch all the charges go by, and you see the number of coulombs that go by per second. That’s called the electric current and is measured in amperes. So 1 coulomb per second is 1 amp.
So Electric Current is the rate of flow of an electric charge per unit time in a conducing wire.
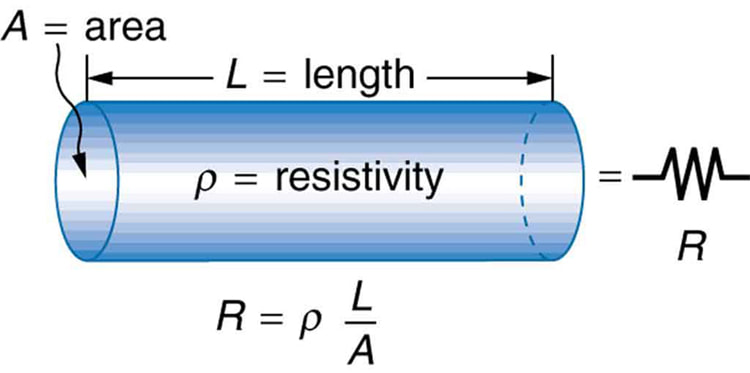
2) Resistance (R)
Resistance (R): Resistance is the measurement of how much a conductive material (like copper) for example resists the flow of charge (like electrons) in a wire or circuit.
Technically speaking, Resistance is due to electrons in a conductor colliding with the ionic lattice of the conductor meaning that electrical energy is converted into heat. Different materials have different resistivities (a property defining how resistive a material of given dimensions will be). As you might guess, the best conductors like copper, silver and gold have the lowest resistances. NOTE: Conductivity is the reciprocal of resistivity as it should be. SO Good conductors that have a small resistivity will have a LARGE conductivity which is a measure of how well the electrons flow.
Besides the material, the OTHER Part of the resistance in a circuit is from the geometry of the wire itself, mainly the length and cross sectional area of the wire. So keeping the material the same, thinner and longer wire have larger resistance and Thicker and short wires will have a smaller.
So the overall formula for Resistance in a wire is R = p*L/A.
*This will have an important consequence in PEMF therapy devices as the "good" ones use copper wire. BUT cheaper PEMF companies use THIN wire which has a greater resistance, more heat loss and yields signal that is not clear. We'll explore this in future modules.
NOTE: Impedance is the more general term for the effective resistance of an AC electric circuit arising from the combined effects of BOTH ohmic resistance and reactance. We will do a separate VIDEO at some point on AC circuit theory but it is much more complex (pun intended as we need complex numbers).
2) Resistance (R)
Resistance (R): Resistance is the measurement of how much a conductive material (like copper) for example resists the flow of charge (like electrons) in a wire or circuit.
Technically speaking, Resistance is due to electrons in a conductor colliding with the ionic lattice of the conductor meaning that electrical energy is converted into heat. Different materials have different resistivities (a property defining how resistive a material of given dimensions will be). As you might guess, the best conductors like copper, silver and gold have the lowest resistances. NOTE: Conductivity is the reciprocal of resistivity as it should be. SO Good conductors that have a small resistivity will have a LARGE conductivity which is a measure of how well the electrons flow.
Besides the material, the OTHER Part of the resistance in a circuit is from the geometry of the wire itself, mainly the length and cross sectional area of the wire. So keeping the material the same, thinner and longer wire have larger resistance and Thicker and short wires will have a smaller.
So the overall formula for Resistance in a wire is R = p*L/A.
*This will have an important consequence in PEMF therapy devices as the "good" ones use copper wire. BUT cheaper PEMF companies use THIN wire which has a greater resistance, more heat loss and yields signal that is not clear. We'll explore this in future modules.
NOTE: Impedance is the more general term for the effective resistance of an AC electric circuit arising from the combined effects of BOTH ohmic resistance and reactance. We will do a separate VIDEO at some point on AC circuit theory but it is much more complex (pun intended as we need complex numbers).
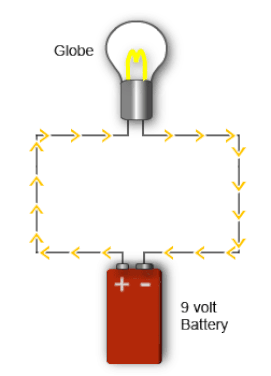
3) Voltage Revisited (in relation to circuits).
Once Charges are Separated, the Voltage Represents Stored ENERGY!! (think Battery)
Voltage is the term used to describe electrical pressure in a circuit.
A battery has a build up of negative charge at one terminal and positive charge at the other. These charges want to balance out, so there is an electrical pressure or force between them (called the electromotive force).
When a circuit is connected between the terminals of a battery, the electrical pressure (voltage) from the battery forces electrons to flow from the negative terminal to the positive terminal.
In a battery, electrons are chemically separated out to the (-) side and prevented from leaking on to the (+) side through the inside.
So there's pressure built up for electrons to move from - to + around a circuit.
Between the positive and negative terminals of the battery there are some chemicals that essentially remove electrons from the positive terminal and deposit them on the negative terminal. Finally chemical forces balance electrostatic field and final voltage is reached.
NOTE: Usually PEMF devices that are battery powered are NOT strong enough. That is most common batteries do not have enough power to give an effectively strong signal. So I recommend AVOIDING battery powered PEMF devices.
Once Charges are Separated, the Voltage Represents Stored ENERGY!! (think Battery)
Voltage is the term used to describe electrical pressure in a circuit.
A battery has a build up of negative charge at one terminal and positive charge at the other. These charges want to balance out, so there is an electrical pressure or force between them (called the electromotive force).
When a circuit is connected between the terminals of a battery, the electrical pressure (voltage) from the battery forces electrons to flow from the negative terminal to the positive terminal.
In a battery, electrons are chemically separated out to the (-) side and prevented from leaking on to the (+) side through the inside.
So there's pressure built up for electrons to move from - to + around a circuit.
Between the positive and negative terminals of the battery there are some chemicals that essentially remove electrons from the positive terminal and deposit them on the negative terminal. Finally chemical forces balance electrostatic field and final voltage is reached.
NOTE: Usually PEMF devices that are battery powered are NOT strong enough. That is most common batteries do not have enough power to give an effectively strong signal. So I recommend AVOIDING battery powered PEMF devices.
Electromotive Force (Voltage or Driving Force in a Circuit)
The EMF in a battery has the same units as voltage and it is the driving force that moves charges.
You can think of many different types of voltage sources. Batteries themselves come in many varieties. There are many types of mechanical/electrical generators, driven by many different energy sources, ranging from nuclear to wind. Solar cells create voltages directly from light, while thermoelectric devices create voltage from temperature differences.
There are really two forces involved in driving current around a circuit: the source, F, which is ordinarily confined to one portion of the loop (a battery say), and an electromotive force which serves to smooth out the flow and communicate the influence of the source to distant parts of the circuit.
F (main driving force of the circuit) can be:
All such devices create a potential difference and can supply current if connected to a resistance. On the small scale, the potential difference creates an electric field that exerts force on charges, causing current. We thus use the name electromotive force, abbreviated emf. Emf is not a force at all; it is a special type of potential difference. To be precise, the electromotive force (emf) is the potential difference of a source when no current is flowing. Units of emf are volts.
The EMF in a battery has the same units as voltage and it is the driving force that moves charges.
You can think of many different types of voltage sources. Batteries themselves come in many varieties. There are many types of mechanical/electrical generators, driven by many different energy sources, ranging from nuclear to wind. Solar cells create voltages directly from light, while thermoelectric devices create voltage from temperature differences.
There are really two forces involved in driving current around a circuit: the source, F, which is ordinarily confined to one portion of the loop (a battery say), and an electromotive force which serves to smooth out the flow and communicate the influence of the source to distant parts of the circuit.
F (main driving force of the circuit) can be:
- a battery which is a chemical force
- A piezpelectric crystal mechanical pressure converted to an electrical impulse
- A thermocouple where temperature gradient does the work
- A photoelectric cell like solar panels where LIGHT does the job
- Generators of All kinds that where a wire is moved through a magnetic field and a current is INDUCED (electromagnetic induction). This is EMF w/o a battery. This EMF comes purely from a Changing Magnetic field. More on this later.
All such devices create a potential difference and can supply current if connected to a resistance. On the small scale, the potential difference creates an electric field that exerts force on charges, causing current. We thus use the name electromotive force, abbreviated emf. Emf is not a force at all; it is a special type of potential difference. To be precise, the electromotive force (emf) is the potential difference of a source when no current is flowing. Units of emf are volts.
The current that flows through most substances is directly proportional to the voltage V applied to it. The German physicist Georg Simon Ohm (1787–1854) was the first to demonstrate experimentally that the current in a metal wire is directly proportional to the voltage applied:
I is proportional to V
This important relationship is known as Ohm’s law. It can be viewed as a cause-and-effect relationship, with voltage the cause and current the effect. This is an empirical law like that for friction—an experimentally observed phenomenon. Such a linear relationship doesn’t always occur.
If voltage drives current, what impedes it? The electric property that impedes current (crudely similar to friction and air resistance) is called resistance R. Collisions of moving charges with atoms and molecules in a substance transfer energy to the substance and limit current.
Resistance is defined as inversely proportional to current.
Thus, for example, current is cut in half if resistance doubles. Combining the relationships of current to voltage and current to resistance gives
I = V/R
This relationship is also called Ohm’s law. Ohm’s law in this form really defines resistance for certain materials. Ohm’s law (like Hooke’s law) is not universally valid. The many substances for which Ohm’s law holds are called ohmic. These include good conductors like copper and aluminum
I is proportional to V
This important relationship is known as Ohm’s law. It can be viewed as a cause-and-effect relationship, with voltage the cause and current the effect. This is an empirical law like that for friction—an experimentally observed phenomenon. Such a linear relationship doesn’t always occur.
If voltage drives current, what impedes it? The electric property that impedes current (crudely similar to friction and air resistance) is called resistance R. Collisions of moving charges with atoms and molecules in a substance transfer energy to the substance and limit current.
Resistance is defined as inversely proportional to current.
Thus, for example, current is cut in half if resistance doubles. Combining the relationships of current to voltage and current to resistance gives
I = V/R
This relationship is also called Ohm’s law. Ohm’s law in this form really defines resistance for certain materials. Ohm’s law (like Hooke’s law) is not universally valid. The many substances for which Ohm’s law holds are called ohmic. These include good conductors like copper and aluminum
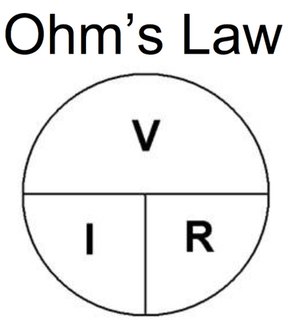
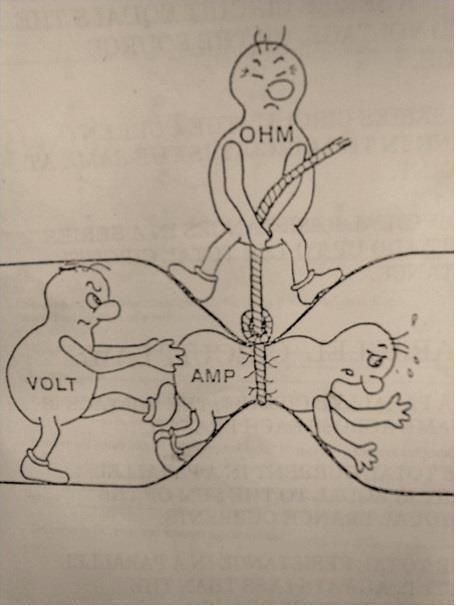
Ohm’s Law:
The aforementioned four properties (current, voltage, resistance and power) are all fundamental in diagnosing and designing electrical circuits. With only two of the above values, you can figure out any other value. This is ohm’s law.
V = I*R
I = V/R
R = V/I
P = V*I or P = (I*I)*R
A voltage of One Volt, will force a current of One Amp, through a resistance of One Ohm, which will create One Watt of power!
The aforementioned four properties (current, voltage, resistance and power) are all fundamental in diagnosing and designing electrical circuits. With only two of the above values, you can figure out any other value. This is ohm’s law.
V = I*R
I = V/R
R = V/I
P = V*I or P = (I*I)*R
A voltage of One Volt, will force a current of One Amp, through a resistance of One Ohm, which will create One Watt of power!
Watch This Short Video to See How DC Circuits work with Electric Cars Demonstrating Ohms Law!
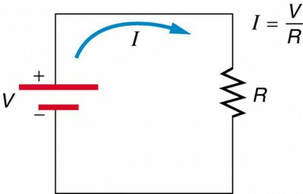
This Figure shows the schematic for a simple circuit. A simple circuit has a single voltage source and a single resistor. The wires connecting the voltage source to the resistor can be assumed to have negligible resistance, or their resistance can be included in R.
A simple electric circuit in which a closed path for current to flow is supplied by conductors (usually metal wires) connecting a load to the terminals of a battery, represented by the red parallel lines. The zigzag symbol represents the single resistor and includes any resistance in the connections to the voltage source.
A simple electric circuit in which a closed path for current to flow is supplied by conductors (usually metal wires) connecting a load to the terminals of a battery, represented by the red parallel lines. The zigzag symbol represents the single resistor and includes any resistance in the connections to the voltage source.
Series Circuits Introduction
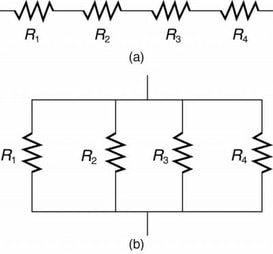
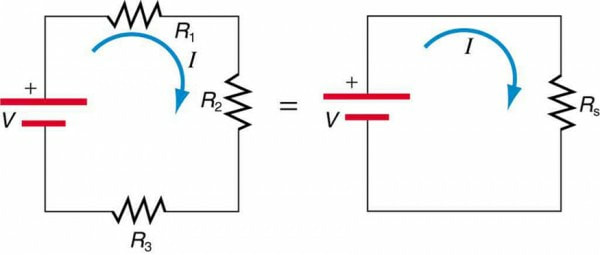
When are resistors in series? Resistors are in series whenever the flow of charge, called the current, must flow through devices sequentially. For example, if current flows through a person holding a screwdriver and into the Earth, then R1 in Figure 1(a) could be the resistance of the screwdriver’s shaft, R2 the resistance of its handle, R3 the person’s body resistance, and R4 the resistance of her shoes. This figure shows resistors in series connected to a voltage source. It seems reasonable that the total resistance is the sum of the individual resistances, considering that the current has to pass through each resistor in sequence. (This fact would be an advantage to a person wishing to avoid an electrical shock, who could reduce the current by wearing high-resistance rubber-soled shoes. It could be a disadvantage if one of the resistances were a faulty high-resistance cord to an appliance that would reduce the operating current.)
To verify that resistances in series do indeed add, let us consider the loss of electrical power, called a voltage drop, in each resistor in Figure below. According to Ohm’s law, the voltage drop, V, across a resistor when a current flows through it is calculated using the equation V = IR, where I equals the current in amps (A) and R is the resistance in ohms (Ω). Another way to think of this is that V is the voltage necessary to make a current I flow through a resistance R. So the voltage drop across R1 is V1 = IR1, that across R2 is V2 = IR2, and that across R3 is V3 = IR3. The sum of these voltages equals the voltage output of the source; that is, V = V1 + V2 + V3.
This equation is based on the conservation of energy and conservation of charge. Electrical potential energy can be described by the equation PE = qV, where q is the electric charge and V is the voltage. Thus the energy supplied by the source is qV, while that dissipated by the resistors is qV1 + qV2 + qV3.
Three resistors connected in series to a battery (left) and the equivalent single or series resistance (BELOW).
This equation is based on the conservation of energy and conservation of charge. Electrical potential energy can be described by the equation PE = qV, where q is the electric charge and V is the voltage. Thus the energy supplied by the source is qV, while that dissipated by the resistors is qV1 + qV2 + qV3.
Three resistors connected in series to a battery (left) and the equivalent single or series resistance (BELOW).
These energies must be equal, because there is no other source and no other destination for energy in the circuit. Thus, qV = qV1 + qV2 + qV3. The charge q cancels, yielding V = V1 + V2 + V3, as stated. (Note that the same amount of charge passes through the battery and each resistor in a given amount of time, since there is no capacitance to store charge, there is no place for charge to leak, and charge is conserved.) Now substituting the values for the individual voltages gives
V = IR1 + IR2 + IR3 = I(R1 + R2 + R3).
Note that for the equivalent single series resistance Rs, we have
V = IRs.
This implies that the total or equivalent series resistance Rs of three resistors is Rs = R1 + R2 + R3. This logic is valid in general for any number of resistors in series; thus, the total resistance Rs of a series connection is
Rs = R1 + R2 + R3+…,
as proposed. Since all of the current must pass through each resistor, it experiences the resistance of each, and resistances in series simply add up.
V = IR1 + IR2 + IR3 = I(R1 + R2 + R3).
Note that for the equivalent single series resistance Rs, we have
V = IRs.
This implies that the total or equivalent series resistance Rs of three resistors is Rs = R1 + R2 + R3. This logic is valid in general for any number of resistors in series; thus, the total resistance Rs of a series connection is
Rs = R1 + R2 + R3+…,
as proposed. Since all of the current must pass through each resistor, it experiences the resistance of each, and resistances in series simply add up.
Parallel Circuits Introduction
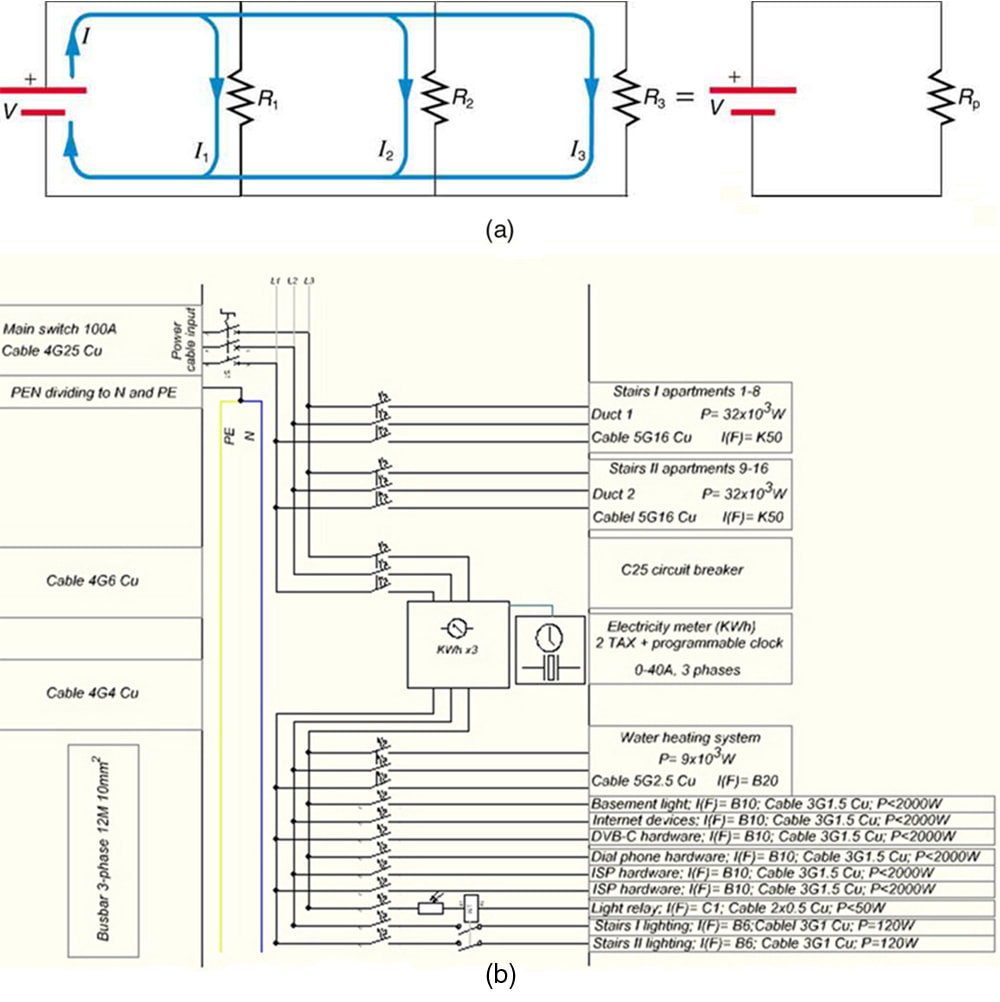
Figure Below shows resistors in parallel, wired to a voltage source. Resistors are in parallel when each resistor is connected directly to the voltage source by connecting wires having negligible resistance. Each resistor thus has the full voltage of the source applied to it. Each resistor draws the same current it would if it alone were connected to the voltage source (provided the voltage source is not overloaded). For example, an automobile’s headlights, radio, and so on, are wired in parallel, so that they utilize the full voltage of the source and can operate completely independently. The same is true in your house, or any building. (See Figure below (b).)
(a) Three resistors connected in parallel to a battery and the equivalent single or parallel resistance. (b) Electrical power setup in a house. (credit: Dmitry G, Wikimedia Commons)
Figure Below shows resistors in parallel, wired to a voltage source. Resistors are in parallel when each resistor is connected directly to the voltage source by connecting wires having negligible resistance. Each resistor thus has the full voltage of the source applied to it. Each resistor draws the same current it would if it alone were connected to the voltage source (provided the voltage source is not overloaded). For example, an automobile’s headlights, radio, and so on, are wired in parallel, so that they utilize the full voltage of the source and can operate completely independently. The same is true in your house, or any building. (See Figure below (b).)
(a) Three resistors connected in parallel to a battery and the equivalent single or parallel resistance. (b) Electrical power setup in a house. (credit: Dmitry G, Wikimedia Commons)
To find an expression for the equivalent parallel resistance Rp, let us consider the currents that flow and how they are related to resistance. Since each resistor in the circuit has the full voltage, the currents flowing through the individual resistors are
I1 = V/R1
I2 = V/R2
I3 = V/R3
Conservation of charge implies that the total current I produced by the source is the sum of these currents:
I = I1 + I2 + I3.
Substituting the expressions for the individual currents gives
I = V/R1 + V/R2 + V/R3 = V*(1/R1 + 1/R2 + 1/R3)
Note that Ohm’s law for the equivalent single resistance gives
I = V/Rp = V*(1/Rp)
The terms inside the parentheses in the last two equations must be equal. Generalizing to any number of resistors, the total resistance Rp of a parallel connection is related to the individual resistances by
1/Rp = 1/R1 + 1/R2 + 1/R3...
This relationship results in a total resistance Rp that is less than the smallest of the individual resistances. (This is seen in the next example.) When resistors are connected in parallel, more current flows from the source than would flow for any of them individually, and so the total resistance is lower.
I1 = V/R1
I2 = V/R2
I3 = V/R3
Conservation of charge implies that the total current I produced by the source is the sum of these currents:
I = I1 + I2 + I3.
Substituting the expressions for the individual currents gives
I = V/R1 + V/R2 + V/R3 = V*(1/R1 + 1/R2 + 1/R3)
Note that Ohm’s law for the equivalent single resistance gives
I = V/Rp = V*(1/Rp)
The terms inside the parentheses in the last two equations must be equal. Generalizing to any number of resistors, the total resistance Rp of a parallel connection is related to the individual resistances by
1/Rp = 1/R1 + 1/R2 + 1/R3...
This relationship results in a total resistance Rp that is less than the smallest of the individual resistances. (This is seen in the next example.) When resistors are connected in parallel, more current flows from the source than would flow for any of them individually, and so the total resistance is lower.
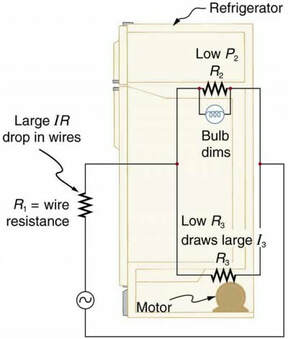
More Complex Connections.
More complex connections of resistors are sometimes just combinations of series and parallel. These are commonly encountered, especially when wire resistance is considered. In that case, wire resistance is in series with other resistances that are in parallel.
For example your refrigerator is a combination of parallel and series resistors.
Resistance in wires reduces the current and power delivered to a resistor. If wire resistance is relatively large, as in a worn (or a very long) extension cord, then this loss can be significant. If a large current is drawn, the IR drop in the wires can also be significant.
For example, when you are rummaging in the refrigerator and the motor comes on, the refrigerator light dims momentarily. Similarly, you can see the passenger compartment light dim when you start the engine of your car (although this may be due to resistance inside the battery itself).
What is happening in these high-current situations is illustrated in Figure 6. The device represented by R3 has a very low resistance, and so when it is switched on, a large current flows. This increased current causes a larger IR drop in the wires represented by R1, reducing the voltage across the light bulb (which is R2), which then dims noticeably.
More complex connections of resistors are sometimes just combinations of series and parallel. These are commonly encountered, especially when wire resistance is considered. In that case, wire resistance is in series with other resistances that are in parallel.
For example your refrigerator is a combination of parallel and series resistors.
Resistance in wires reduces the current and power delivered to a resistor. If wire resistance is relatively large, as in a worn (or a very long) extension cord, then this loss can be significant. If a large current is drawn, the IR drop in the wires can also be significant.
For example, when you are rummaging in the refrigerator and the motor comes on, the refrigerator light dims momentarily. Similarly, you can see the passenger compartment light dim when you start the engine of your car (although this may be due to resistance inside the battery itself).
What is happening in these high-current situations is illustrated in Figure 6. The device represented by R3 has a very low resistance, and so when it is switched on, a large current flows. This increased current causes a larger IR drop in the wires represented by R1, reducing the voltage across the light bulb (which is R2), which then dims noticeably.
4) Power: Power is the measurement of the rate at which work is actually being preformed by the electrical circuit.
That is the RATE at which ENERGY is consumed. This is what your power company is interested in. The faster you consume energy, the more you have to pay. Knowing that power is the rate of energy use or energy conversion, what is the expression for electric power? Power transmission lines might come to mind. We also think of lightbulbs in terms of their power ratings in watts.
This is measured in Watts (joules/sec). The units are energy per unit time. This can also be compared with Horsepower (1W = 0.0013 HP) and BTU’s (1W = 3.414 BTU/h).
The Cost of Electricity
The more electric appliances you use and the longer they are left on, the higher your electric bill. This familiar fact is based on the relationship between energy and power. You pay for the energy used. Since P = E/t, we see that
E = Pt
is the energy used by a device using power P for a time interval t. For example, the more lightbulbs burning, the greater P used; the longer they are on, the greater t is. The energy unit on electric bills is the kilowatt-hour (kW ⋅ h), consistent with the relationship E = Pt. It is easy to estimate the cost of operating electric appliances if you have some idea of their power consumption rate in watts or kilowatts, the time they are on in hours, and the cost per kilowatt-hour for your electric utility. Kilowatt-hours, like all other specialized energy units such as food calories, can be converted to joules. You can prove to yourself that 1 kW ⋅ h = 3.6 × 106 J.
The electrical energy (E) used can be reduced either by reducing the time of use or by reducing the power consumption of that appliance or fixture. This will not only reduce the cost, but it will also result in a reduced impact on the environment. Improvements to lighting are some of the fastest ways to reduce the electrical energy used in a home or business. About 20% of a home’s use of energy goes to lighting, while the number for commercial establishments is closer to 40%.
Power in Electric Circuits
Electric energy depends on both the voltage involved and the charge moved. This is expressed most simply as PE = qV, where q is the charge moved and V is the voltage (or more precisely, the potential difference the charge moves through). Power is the rate at which energy is moved, and so electric power is
P = PE/t = qV/t
But since I = q/t
We have P = IV
Electric power (P) is simply the product of current times voltage. Power has familiar units of watts. Since the SI unit for potential energy (PE) is the joule, power has units of joules per second, or watts. Thus, 1 A ⋅V= 1 W. For example, cars often have one or more auxiliary power outlets with which you can charge a cell phone or other electronic devices. These outlets may be rated at 20 A, so that the circuit can deliver a maximum power P = IV = (20 A)(12 V) = 240 W.
Back to the analogy with weights, Energy = F*d does not have any time. So power lifters, appropriately called, jerk the weight up VERY fast... This is power Energy/time.
That is the RATE at which ENERGY is consumed. This is what your power company is interested in. The faster you consume energy, the more you have to pay. Knowing that power is the rate of energy use or energy conversion, what is the expression for electric power? Power transmission lines might come to mind. We also think of lightbulbs in terms of their power ratings in watts.
This is measured in Watts (joules/sec). The units are energy per unit time. This can also be compared with Horsepower (1W = 0.0013 HP) and BTU’s (1W = 3.414 BTU/h).
The Cost of Electricity
The more electric appliances you use and the longer they are left on, the higher your electric bill. This familiar fact is based on the relationship between energy and power. You pay for the energy used. Since P = E/t, we see that
E = Pt
is the energy used by a device using power P for a time interval t. For example, the more lightbulbs burning, the greater P used; the longer they are on, the greater t is. The energy unit on electric bills is the kilowatt-hour (kW ⋅ h), consistent with the relationship E = Pt. It is easy to estimate the cost of operating electric appliances if you have some idea of their power consumption rate in watts or kilowatts, the time they are on in hours, and the cost per kilowatt-hour for your electric utility. Kilowatt-hours, like all other specialized energy units such as food calories, can be converted to joules. You can prove to yourself that 1 kW ⋅ h = 3.6 × 106 J.
The electrical energy (E) used can be reduced either by reducing the time of use or by reducing the power consumption of that appliance or fixture. This will not only reduce the cost, but it will also result in a reduced impact on the environment. Improvements to lighting are some of the fastest ways to reduce the electrical energy used in a home or business. About 20% of a home’s use of energy goes to lighting, while the number for commercial establishments is closer to 40%.
Power in Electric Circuits
Electric energy depends on both the voltage involved and the charge moved. This is expressed most simply as PE = qV, where q is the charge moved and V is the voltage (or more precisely, the potential difference the charge moves through). Power is the rate at which energy is moved, and so electric power is
P = PE/t = qV/t
But since I = q/t
We have P = IV
Electric power (P) is simply the product of current times voltage. Power has familiar units of watts. Since the SI unit for potential energy (PE) is the joule, power has units of joules per second, or watts. Thus, 1 A ⋅V= 1 W. For example, cars often have one or more auxiliary power outlets with which you can charge a cell phone or other electronic devices. These outlets may be rated at 20 A, so that the circuit can deliver a maximum power P = IV = (20 A)(12 V) = 240 W.
Back to the analogy with weights, Energy = F*d does not have any time. So power lifters, appropriately called, jerk the weight up VERY fast... This is power Energy/time.
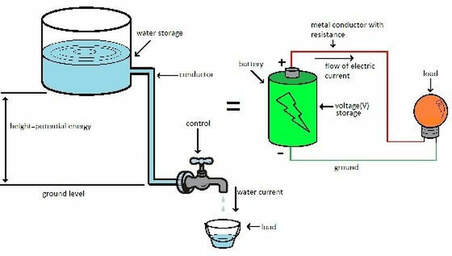
When describing voltage, current, and resistance, a common analogy is a water tank. In this analogy, charge is represented by the water amount, voltage is represented by the water pressure, and current is represented by the water flow. So for this analogy, remember:
Water = Charge
Pressure = Voltage
Flow = Current
I will leave it as an exercise for you to contemplate this analogy. More information BELOW.
Water = Charge
Pressure = Voltage
Flow = Current
I will leave it as an exercise for you to contemplate this analogy. More information BELOW.
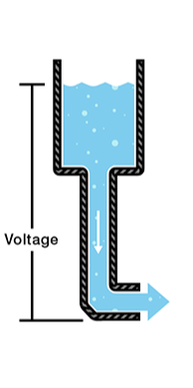
OPTIONAL - More detailed Discussion on Water Tower/Circuit Analogy.
Consider a water tank at a certain height above the ground. At the bottom of this tank there is a hose.The pressure at the end of the hose can represent voltage. The water in the tank represents charge. The more water in the tank, the higher the charge, the more pressure is measured at the end of the hose.
We can think of this tank as a battery, a place where we store a certain amount of energy and then release it. If we drain our tank a certain amount, the pressure created at the end of the hose goes down. We can think of this as decreasing voltage, like when a flashlight gets dimmer as the batteries run down. There is also a decrease in the amount of water that will flow through the hose. Less pressure means less water is flowing, which brings us to current.
Consider a water tank at a certain height above the ground. At the bottom of this tank there is a hose.The pressure at the end of the hose can represent voltage. The water in the tank represents charge. The more water in the tank, the higher the charge, the more pressure is measured at the end of the hose.
We can think of this tank as a battery, a place where we store a certain amount of energy and then release it. If we drain our tank a certain amount, the pressure created at the end of the hose goes down. We can think of this as decreasing voltage, like when a flashlight gets dimmer as the batteries run down. There is also a decrease in the amount of water that will flow through the hose. Less pressure means less water is flowing, which brings us to current.
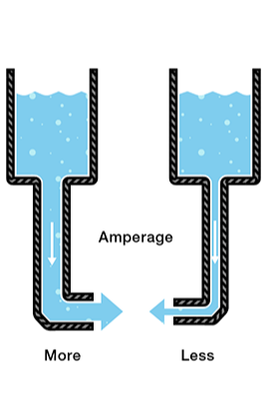
We can think of the amount of water flowing through the hose from the tank as current. The higher the pressure, the higher the flow, and vice-versa. With water, we would measure the volume of the water flowing through the hose over a certain period of time. With electricity, we measure the amount of charge flowing through the circuit over a period of time. Current is measured in Amperes (usually just referred to as “Amps”). An ampere is defined as 6.241*1018 electrons (1 Coulomb) per second passing through a point in a circuit. Amps are represented in equations by the letter “I”.
Let’s say now that we have two tanks, each with a hose coming from the bottom. Each tank has the exact same amount of water, but the hose on one tank is narrower than the hose on the other.
We measure the same amount of pressure at the end of either hose, but when the water begins to flow, the flow rate of the water in the tank with the narrower hose will be less than the flow rate of the water in the tank with the wider hose. In electrical terms, the current through the narrower hose is less than the current through the wider hose. If we want the flow to be the same through both hoses, we have to increase the amount of water (charge) in the tank with the narrower hose.
Let’s say now that we have two tanks, each with a hose coming from the bottom. Each tank has the exact same amount of water, but the hose on one tank is narrower than the hose on the other.
We measure the same amount of pressure at the end of either hose, but when the water begins to flow, the flow rate of the water in the tank with the narrower hose will be less than the flow rate of the water in the tank with the wider hose. In electrical terms, the current through the narrower hose is less than the current through the wider hose. If we want the flow to be the same through both hoses, we have to increase the amount of water (charge) in the tank with the narrower hose.
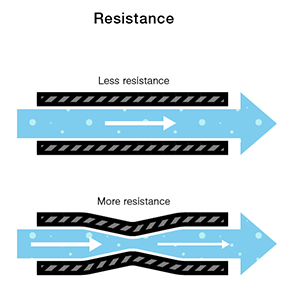
It stands to reason that we can’t fit as much volume through a narrow pipe than a wider one at the same pressure. This is resistance. The narrow pipe “resists” the flow of water through it even though the water is at the same pressure as the tank with the wider pipe.
In electrical terms, this is represented by two circuits with equal voltages and different resistances. The circuit with the higher resistance will allow less charge to flow, meaning the circuit with higher resistance has less current flowing through it.
This brings us back to Georg Ohm. Ohm defines the unit of resistance of “1 Ohm” as the resistance between two points in a conductor where the application of 1 volt will push 1 ampere, or 6.241×1018 electrons. This value is usually represented in schematics with the greek letter “Ω”, which is called omega, and pronounced “ohm”.
Combining the elements of voltage, current, and resistance, Ohm developed the formula:
Where
V = Voltage in volts
I = Current in amps
R = Resistance in ohms
This is called Ohm’s law.
In electrical terms, this is represented by two circuits with equal voltages and different resistances. The circuit with the higher resistance will allow less charge to flow, meaning the circuit with higher resistance has less current flowing through it.
This brings us back to Georg Ohm. Ohm defines the unit of resistance of “1 Ohm” as the resistance between two points in a conductor where the application of 1 volt will push 1 ampere, or 6.241×1018 electrons. This value is usually represented in schematics with the greek letter “Ω”, which is called omega, and pronounced “ohm”.
Combining the elements of voltage, current, and resistance, Ohm developed the formula:
Where
V = Voltage in volts
I = Current in amps
R = Resistance in ohms
This is called Ohm’s law.
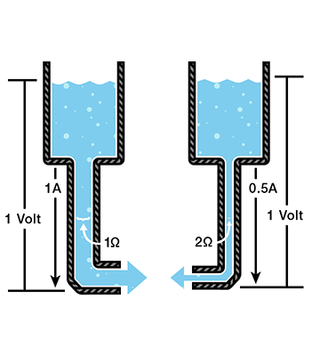
Let’s say, for example, that we have a circuit with the potential of 1 volt, a current of 1 amp, and resistance of 1 ohm. Using Ohm’s Law we can say:
Let’s say this represents our tank with a wide hose. The amount of water in the tank is defined as 1 volt and the “narrowness” (resistance to flow) of the hose is defined as 1 ohm. Using Ohms Law, this gives us a flow (current) of 1 amp.
Using this analogy, let’s now look at the tank with the narrow hose. Because the hose is narrower, its resistance to flow is higher. Let’s define this resistance as 2 ohms. The amount of water in the tank is the same as the other tank, so, using Ohm’s Law, our equation for the tank with the narrow hose is
But what is the current? Because the resistance is greater, and the voltage is the same, this gives us a current value of 0.5 amps:
I will close with this Analogy Applied to the Body and How PEMF Helps to Increase the Bodies Energy...
1) Voltage/Pump - The heart is the source of energy... The Bodies Main Pump or Voltage V Source.
2) Current I is the rate at which blood/plasma/lymph flows. Better current and blood flow means better deliverance of oxygen and nutrients to the cells.
3) R = Resistance and viscosity -
a. length of vessel and cross sectional area (remember resistance equation).
b. Viscosity of blood like the resistivity of material. Thicker blood = more resistance = LESS flow = Poor Health.
Thick blood and small vessels (blocked by bad circulation) increases resistance.
Increased resistance puts back pressure on heart and leads to poor nutrient delivery and detox.
PEMF increases MICROCIRCULATION and both WIDENS blood vessels AND lowers viscosity/surface tension of blood, plasma and lymph.
Let’s say this represents our tank with a wide hose. The amount of water in the tank is defined as 1 volt and the “narrowness” (resistance to flow) of the hose is defined as 1 ohm. Using Ohms Law, this gives us a flow (current) of 1 amp.
Using this analogy, let’s now look at the tank with the narrow hose. Because the hose is narrower, its resistance to flow is higher. Let’s define this resistance as 2 ohms. The amount of water in the tank is the same as the other tank, so, using Ohm’s Law, our equation for the tank with the narrow hose is
But what is the current? Because the resistance is greater, and the voltage is the same, this gives us a current value of 0.5 amps:
I will close with this Analogy Applied to the Body and How PEMF Helps to Increase the Bodies Energy...
1) Voltage/Pump - The heart is the source of energy... The Bodies Main Pump or Voltage V Source.
2) Current I is the rate at which blood/plasma/lymph flows. Better current and blood flow means better deliverance of oxygen and nutrients to the cells.
3) R = Resistance and viscosity -
a. length of vessel and cross sectional area (remember resistance equation).
b. Viscosity of blood like the resistivity of material. Thicker blood = more resistance = LESS flow = Poor Health.
Thick blood and small vessels (blocked by bad circulation) increases resistance.
Increased resistance puts back pressure on heart and leads to poor nutrient delivery and detox.
PEMF increases MICROCIRCULATION and both WIDENS blood vessels AND lowers viscosity/surface tension of blood, plasma and lymph.