VI. Maxwells Equations (Part 1)-
Summarizing Everything Electrical, Magnetic & Electromagnetic
Summarizing Everything Electrical, Magnetic & Electromagnetic
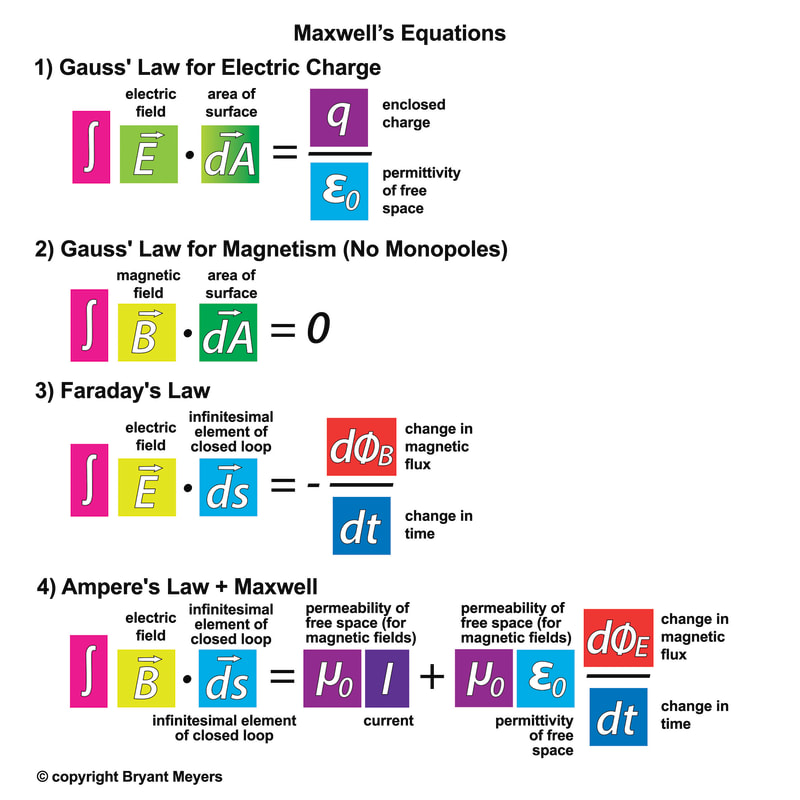
Maxwell's equations are four of the most influential equations in science:
Gauss's law for electric fields, Gauss's law for magnetic fields, Faraday's Law and the Ampere-Maxwell Law, all of which we have seen in simpler forms in earlier modules.
If you need testament of Maxwell's equations, look around you - radio, television, smart phones, radar, computers, wireless internet access, and bluetooth technology are a few examples of contemporary technology rooted in Maxwell's electromagnetic field theory. Little wonder that the readers of Physics World selected Maxwell's equations as "the most important equations of all time".
And for our purpose these 4 equations along with the Lorenz force law contain all the physics needed to understand PEMF devices (and most energy medicine devices as well).
Gauss's law for electric fields, Gauss's law for magnetic fields, Faraday's Law and the Ampere-Maxwell Law, all of which we have seen in simpler forms in earlier modules.
If you need testament of Maxwell's equations, look around you - radio, television, smart phones, radar, computers, wireless internet access, and bluetooth technology are a few examples of contemporary technology rooted in Maxwell's electromagnetic field theory. Little wonder that the readers of Physics World selected Maxwell's equations as "the most important equations of all time".
And for our purpose these 4 equations along with the Lorenz force law contain all the physics needed to understand PEMF devices (and most energy medicine devices as well).
So now let's go through each one briefly. We will stick with the integral forms for simplicity.
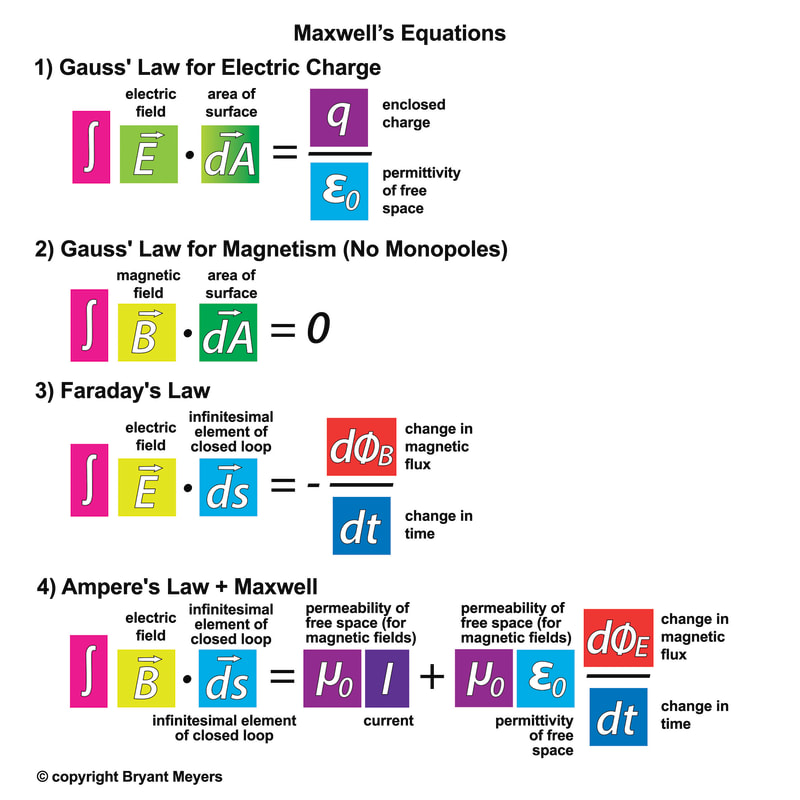
1) Gauss's Law for Electric Fields
First recall that a electric charge creates an electric field which exerts an electric force on other electrically charged particles.
1) Gauss's Law for Electric Fields
First recall that a electric charge creates an electric field which exerts an electric force on other electrically charged particles.
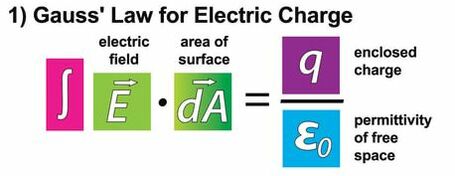
Formally Gauss's Law states:
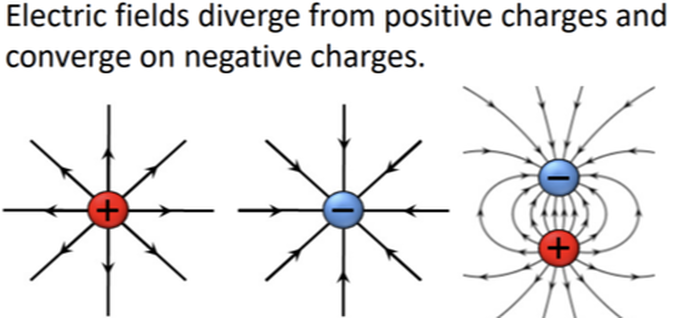
"Electric Charges Produces an Electric Field, and the flux of that field passing through any closed surface is proportional to the total charge contained with that surface."
"Electric Charges Produces an Electric Field, and the flux of that field passing through any closed surface is proportional to the total charge contained with that surface."
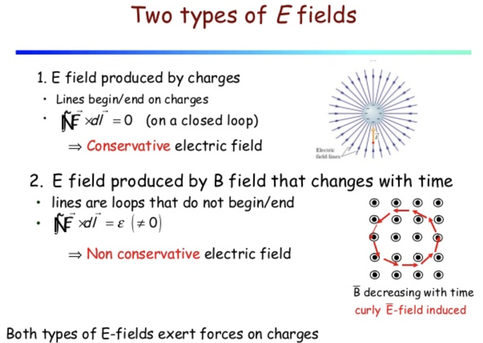
Gauss's Law for electric charge, completely describes the electric field around ANY static charge distribution.
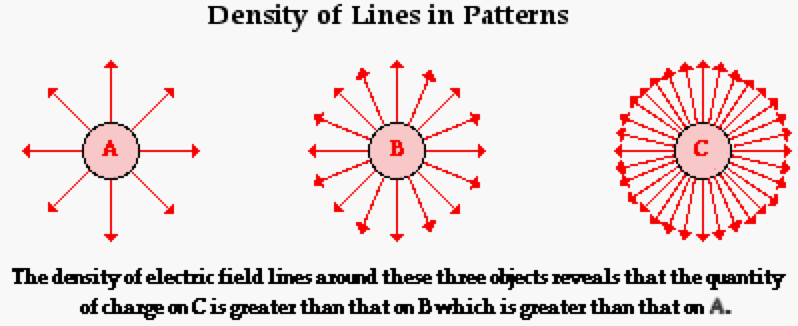
If the math is too hard, that is ok, remember that the electric field strength - VISUALLY - is proportional to the density of electric field lines like in these images. The more densely the flux lines are arranged, the greater the intensity or strength of the field.
If the math is too hard, that is ok, remember that the electric field strength - VISUALLY - is proportional to the density of electric field lines like in these images. The more densely the flux lines are arranged, the greater the intensity or strength of the field.
Remember These two points from the water flow analogy (Flux=Flow)
1) more lines is like greater water pressure (think stronger firehose vs weaker garden hose),
2) and lines pointing out are like a faucet or hose, and lines pointing in are like a sink or drain.
Only instead of water pressure it is electric force pressure (but interesting the equations for both are similar).
Ok that is Maxwell's first equation which is also Coulombs law describing forces between charges, but more generalized and elegant in its formalism.
1) more lines is like greater water pressure (think stronger firehose vs weaker garden hose),
2) and lines pointing out are like a faucet or hose, and lines pointing in are like a sink or drain.
Only instead of water pressure it is electric force pressure (but interesting the equations for both are similar).
Ok that is Maxwell's first equation which is also Coulombs law describing forces between charges, but more generalized and elegant in its formalism.

Maxwell's second equation is also a form of Gauss's law, but in this case with magnetic flux instead of the electric flux.
Gauss's Law for Magnetism states:
The total magnetic flux passing through any closed surface equals zero.
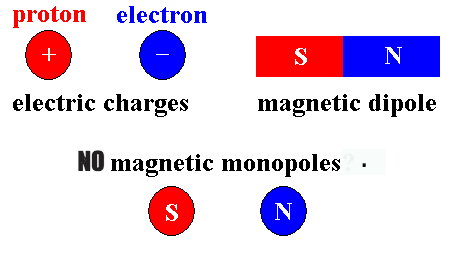
What this means is that there are no magnetic monopoles or stated another way, there is no magnetic charge like positive and negative electric charges (no sources or sinks).
You cannot isolate a North or South Pole, they always appear in pairs.
Where you CAN isolate Positive and negative charge.
Gauss's Law for Magnetism states:
The total magnetic flux passing through any closed surface equals zero.
What this means is that there are no magnetic monopoles or stated another way, there is no magnetic charge like positive and negative electric charges (no sources or sinks).
You cannot isolate a North or South Pole, they always appear in pairs.
Where you CAN isolate Positive and negative charge.
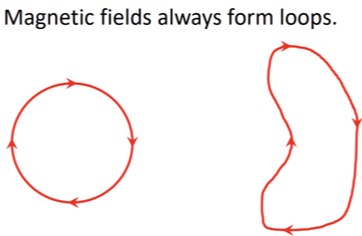
Also Note: Magnetic field lines don't begin or end, they form closed loops which means they cannot be shielded like electric charges or absorbed or reflected like light.
It is THIS property that allows magnetic fields to penetrate deeper and work better therapeutically than electric currents, electric fields and other forms of energy medicine.
It is THIS property that allows magnetic fields to penetrate deeper and work better therapeutically than electric currents, electric fields and other forms of energy medicine.
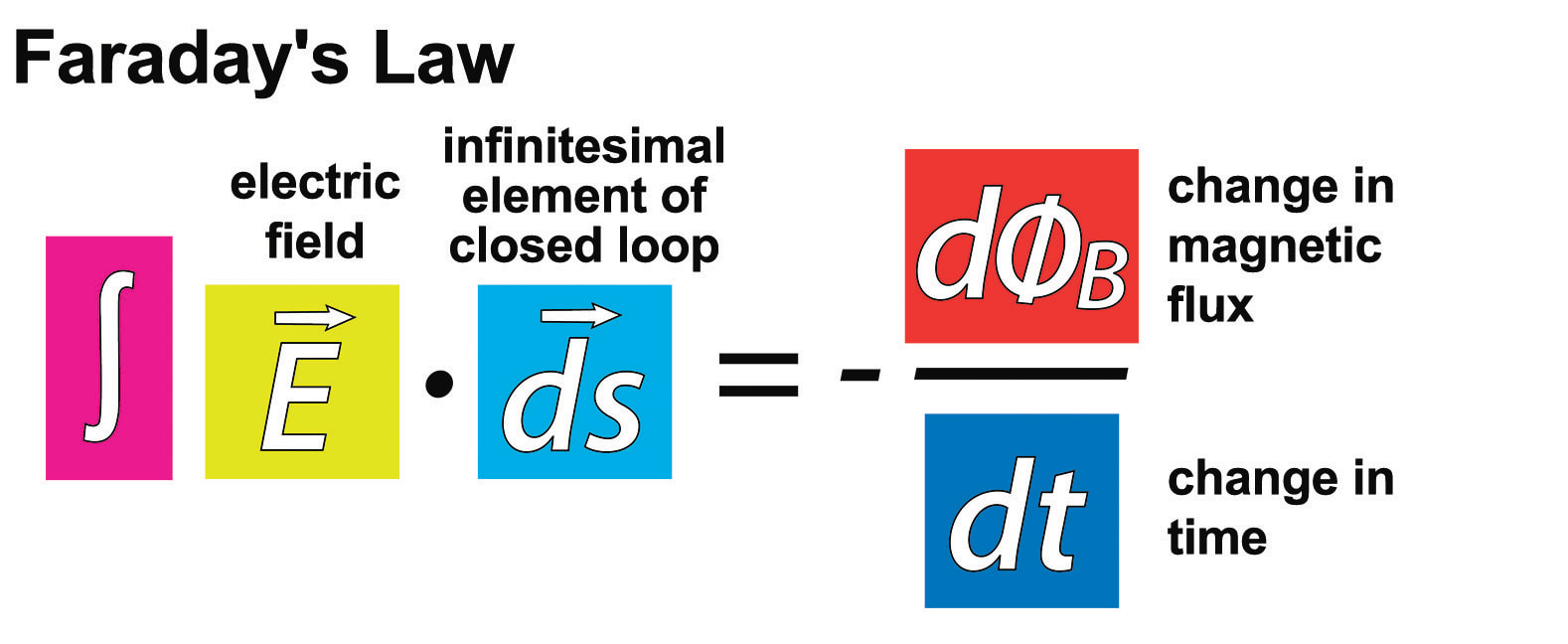
3) Faraday's Law
Remember from Module 6 we saw that Faraday's law of induction says that A changing magnetic field will induce an emf in a loop of wire which then drives the current in that wire.
Maxwell made the assumption that this electric field is present even without the presence of the conducting loop.
So Maxwell's version of Faraday's Law is more general and says that the EMF is equal to the line integral of the electric field over ANY closed loop.
Remember from Module 6 we saw that Faraday's law of induction says that A changing magnetic field will induce an emf in a loop of wire which then drives the current in that wire.
Maxwell made the assumption that this electric field is present even without the presence of the conducting loop.
So Maxwell's version of Faraday's Law is more general and says that the EMF is equal to the line integral of the electric field over ANY closed loop.
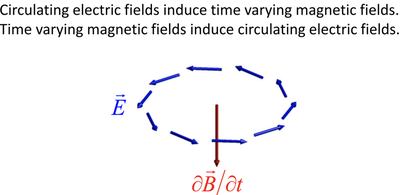
That is, a changing magnetic field induces a CIRCULATING electric field.
And this circulating electric field is the source of the EMF in any circuit, but it can also stand alone in space as a circulating electric field.
This is also called and Eddy Current which means a spinning, twisting or vortexing.
The direction of the EMF opposes the change per Lenz's law. This third of Maxwell’s equations is Faraday’s law of induction, and includes Lenz’s law.
And this circulating electric field is the source of the EMF in any circuit, but it can also stand alone in space as a circulating electric field.
This is also called and Eddy Current which means a spinning, twisting or vortexing.
The direction of the EMF opposes the change per Lenz's law. This third of Maxwell’s equations is Faraday’s law of induction, and includes Lenz’s law.
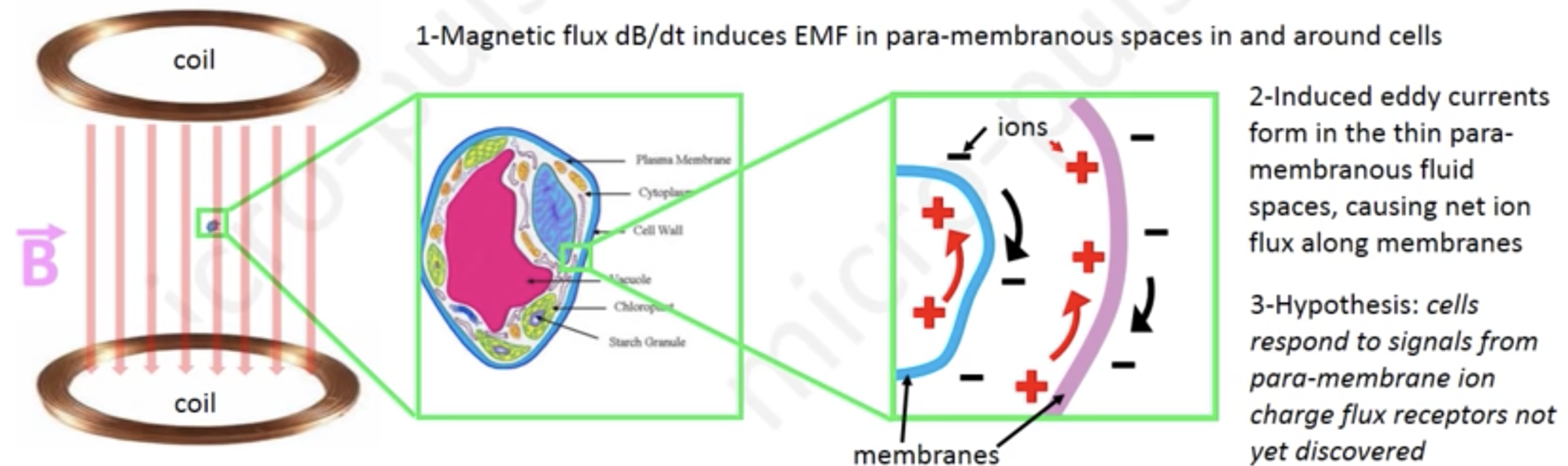
**PEMF NOTE:
All PEMF devices operate and affect the cells on the basis of Faraday's Law of Induction.
The faster the magnetic flux changes (which means a Greater dB/dt), the larger the magnitude of the circulation of the induced Electric Field in your tissues for maximal Ion transport, charge separation and energy production. But note that a rapid rise and fall signal along with frequency resonance is the key to effective (and safe) PEMF applications.
Using PEMF coils to induce Circulating or Eddy Currents that move charged particles like Na and K around the cells, additionally has an effect similar to exercise. Hence PEMF therapy is Cellular Exercise.
All PEMF devices operate and affect the cells on the basis of Faraday's Law of Induction.
The faster the magnetic flux changes (which means a Greater dB/dt), the larger the magnitude of the circulation of the induced Electric Field in your tissues for maximal Ion transport, charge separation and energy production. But note that a rapid rise and fall signal along with frequency resonance is the key to effective (and safe) PEMF applications.
Using PEMF coils to induce Circulating or Eddy Currents that move charged particles like Na and K around the cells, additionally has an effect similar to exercise. Hence PEMF therapy is Cellular Exercise.
PEMF Devices Creating Healthy Eddy Currents in The Cells
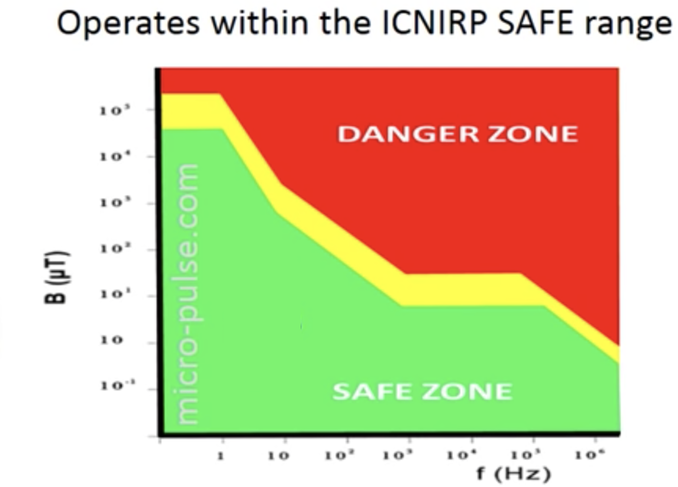
High Intensity PEMF with .1-3 Tesla (1000 - 30,000 gauss) intensities creates circulation Eddy Currents in your body that are WAY TOO Strong and Can Damage the Cells, Tissues and Organs with prolonged and regular use.
This is PHYSICS!
This is PHYSICS!
PROVEN Dangers of High Intensity PEMF
ICNIRP stands for the international commission on non-ionizing radiation protection.
This generally relates to the allowable environmental exposures that people can have to background levels of non-ionizing radiation like radio waves (not x-rays, or nuclear radiation, that is ionizing).
The ICNIRP guidelines are widely used internationally to determine what levels of background radio frequency radiation are acceptable for long term exposure.
The red zone in the chart in this chart is considered the danger zone, that won't necessary hurt you, but there is some scientific reason to believe that it is not good to be in an environment with those levels of radiation.
That is a combination of the strength of the magnetic field and the frequency.
As the magnetic field strength goes up or the frequency goes up, the radiation becomes potentially more dangerous.
Yellow area is the uncertain zone. And the green area is considered absolutely safe meaning there is no scientific evidence that there would be any harm done to a biological system with that level of background radio frequency energy.
ALL HIGH INTENSITY DEVICES ARE IN THE RED ZONE - ALL OF THEM!!!
ICNIRP stands for the international commission on non-ionizing radiation protection.
This generally relates to the allowable environmental exposures that people can have to background levels of non-ionizing radiation like radio waves (not x-rays, or nuclear radiation, that is ionizing).
The ICNIRP guidelines are widely used internationally to determine what levels of background radio frequency radiation are acceptable for long term exposure.
The red zone in the chart in this chart is considered the danger zone, that won't necessary hurt you, but there is some scientific reason to believe that it is not good to be in an environment with those levels of radiation.
That is a combination of the strength of the magnetic field and the frequency.
As the magnetic field strength goes up or the frequency goes up, the radiation becomes potentially more dangerous.
Yellow area is the uncertain zone. And the green area is considered absolutely safe meaning there is no scientific evidence that there would be any harm done to a biological system with that level of background radio frequency energy.
ALL HIGH INTENSITY DEVICES ARE IN THE RED ZONE - ALL OF THEM!!!
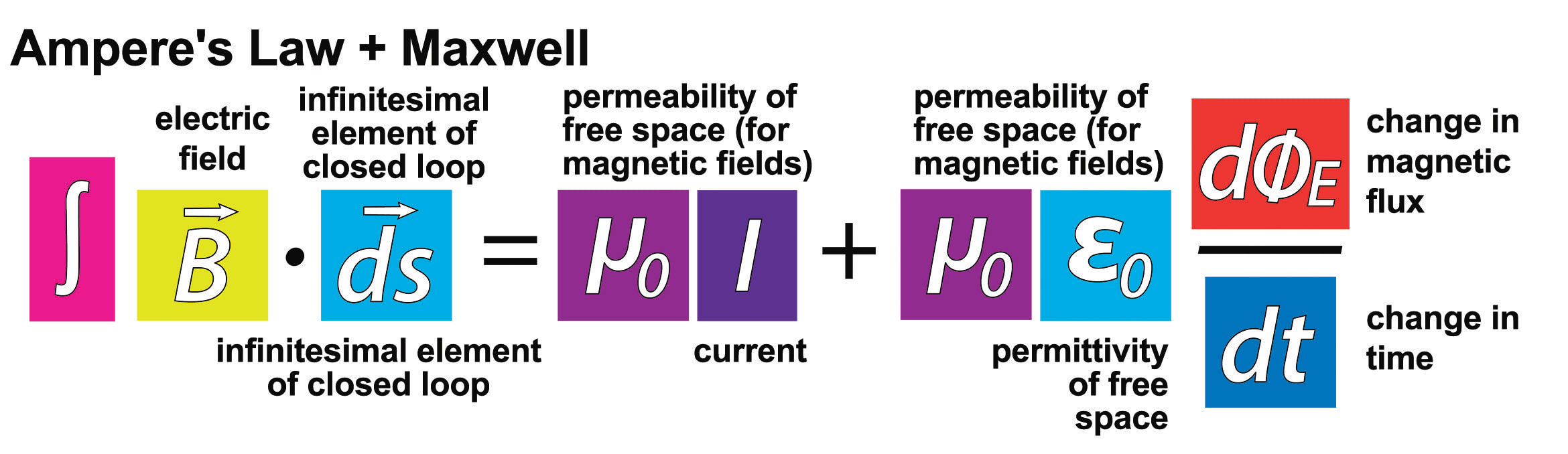
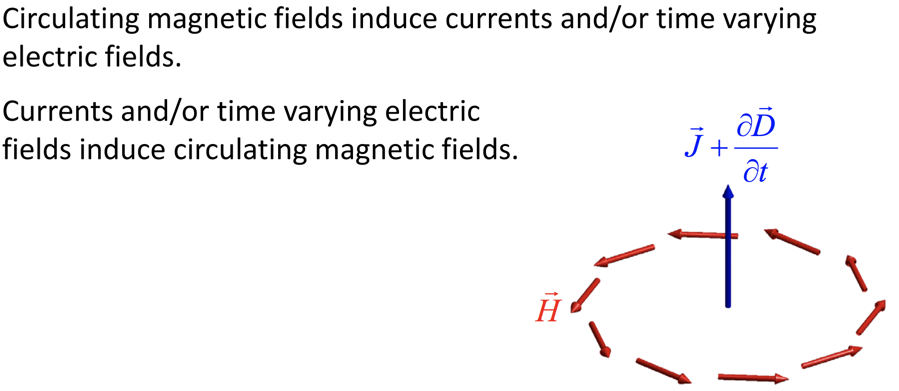
4) Ampere's Law w/ Maxwell Displacement Current
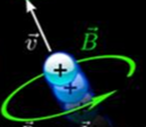
4) The Fourth Maxwell Equation is Ampere's law which says that moving charges, like an electric current in wire, produce a magnetic field (as we saw in Module #5).
And this includes magnetized material as all magnets are a result of circulating electrons (which are little microscopic currents at the atomic level).
In addition to a moving charges, a changing electric field can also produce a magnetic field (This is called Maxwell's Displacement Current which is something NEW to this module).
And this includes magnetized material as all magnets are a result of circulating electrons (which are little microscopic currents at the atomic level).
In addition to a moving charges, a changing electric field can also produce a magnetic field (This is called Maxwell's Displacement Current which is something NEW to this module).
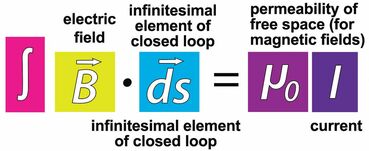
More Formally, the Ampere-Maxwell Law in Integral Form States:
The electric current or changing electric flux through a surface produces a circulating magnetic field around any path that bounds that surface.
This Fourth and Final equation is the one Maxwell made the most tweaks to, in order to make it applicable to ALL electromagnetic phenomena.
Maxwell's first and second equations were so similar - one for electric fields and one for magnetic fields - that he knew there must be an equation that complemented Faraday's Law as Well.
After all, if a changing magnetic flux produces an electric field, why is there not a complementary law saying the reverse? Indeed there is...
The electric current or changing electric flux through a surface produces a circulating magnetic field around any path that bounds that surface.
This Fourth and Final equation is the one Maxwell made the most tweaks to, in order to make it applicable to ALL electromagnetic phenomena.
Maxwell's first and second equations were so similar - one for electric fields and one for magnetic fields - that he knew there must be an equation that complemented Faraday's Law as Well.
After all, if a changing magnetic flux produces an electric field, why is there not a complementary law saying the reverse? Indeed there is...
Let's Behold these marvelous Equations One Last Time... Really Soak them in your subconscious and wonder at the beauty and symmetry of Nature. If this is the first time you have seen Maxwell's equations, REMEMBER THIS DAY!
These Four Equations Of Maxwell TOGETHER with the Force Law
F = q(E + v x B)
Summarize the ENTIRETY of Classical Electrodynamics!
That is everything Electric, Magnetic and Electromagnetic!
These Four Equations Of Maxwell TOGETHER with the Force Law
F = q(E + v x B)
Summarize the ENTIRETY of Classical Electrodynamics!
That is everything Electric, Magnetic and Electromagnetic!
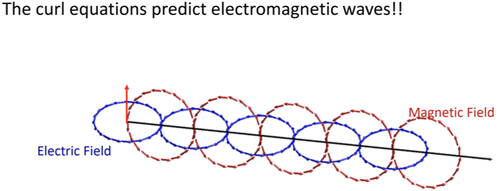
With the addition he made to Ampere's law, Maxwell's equations were complete... And from them we can see a pattern in the production of both electric and magnetic fields and how the two are connected.
If a changing electric field is generated, then a magnetic field is induced, which results in a changing magnetic field that induces an electric field, and the cycle continues.
These oscillations are electromagnetic waves, and they're made up of changing electric and magnetic fields that travel through space.
Maxwell believed that we could reproduce electromagnetic waves AKA LIGHT in the laboratory and he was right!
Let's now briefly explore how LIGHT comes from Maxwell's Equations!
If a changing electric field is generated, then a magnetic field is induced, which results in a changing magnetic field that induces an electric field, and the cycle continues.
These oscillations are electromagnetic waves, and they're made up of changing electric and magnetic fields that travel through space.
Maxwell believed that we could reproduce electromagnetic waves AKA LIGHT in the laboratory and he was right!
Let's now briefly explore how LIGHT comes from Maxwell's Equations!
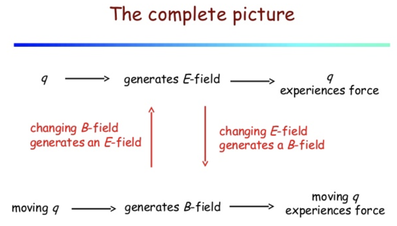
In THIS form, they reinforce the notion that electric fields can be produced EITHER by CHARGES (particles) OR by changing magnetic Fields (waves),
AND magnetic fields can be produced either by currents/moving charges (particles) OR changing electric fields (waves).
But ultimately ALL fields come from charges and currents (moving charges) or that is Charges.
Maxwell's equations really show how charges (stationary or moving)/particles produce FIELDS (waves)!!
The Force Law reciprocally tells you how FIELDS (waves) affect charges (particles)!
So you see Electricity and Magnetism are related to each other and can be looked upon as two facets of what is called electromagnetism which includes as we'll see next, electromagnetic waves.
AND magnetic fields can be produced either by currents/moving charges (particles) OR changing electric fields (waves).
But ultimately ALL fields come from charges and currents (moving charges) or that is Charges.
Maxwell's equations really show how charges (stationary or moving)/particles produce FIELDS (waves)!!
The Force Law reciprocally tells you how FIELDS (waves) affect charges (particles)!
So you see Electricity and Magnetism are related to each other and can be looked upon as two facets of what is called electromagnetism which includes as we'll see next, electromagnetic waves.
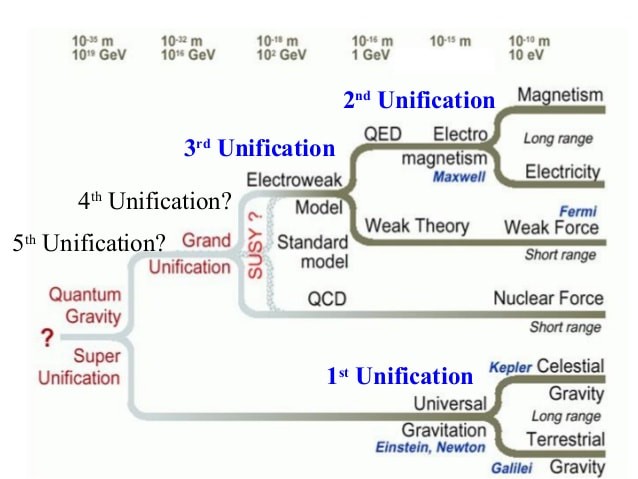
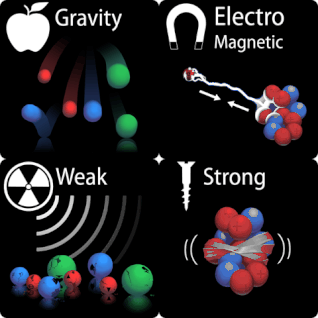
MAKING CONNECTIONS: UNIFICATION OF FORCES
Maxwell’s complete and symmetric theory showed that electric and magnetic forces are not separate, but different manifestations of the same thing—the electromagnetic force. This classical unification of forces is one motivation for current attempts to unify the four basic forces in nature—the gravitational, electrical, strong, and weak nuclear forces.
Maxwell’s complete and symmetric theory showed that electric and magnetic forces are not separate, but different manifestations of the same thing—the electromagnetic force. This classical unification of forces is one motivation for current attempts to unify the four basic forces in nature—the gravitational, electrical, strong, and weak nuclear forces.
Symmetry is apparent in nature in a wide range of situations. In contemporary research, symmetry plays a major part in the search for sub-atomic particles using massive multinational particle accelerators such as the new Large Hadron Collider at CERN.
Due to this intimacy the two are considered two different manifestations of the same unified force called an Electromagnetic Force or EM force. The unified form of an electric and magnetic field is called an EM field, and the electric and magnetic field are considered its components. In other words, an EM force is exerted by an EM field.
Where there is a force, there is energy. The energy corresponding to an EM force is called EM energy or radiation. This energy is transferred from one point in space to another through what are called EM waves.
Light
An electromagnetic wave carries energy and momentum.
The average power per unit area is called the intensity of the wave.
The momentum per unit time (that is, force) per unit area is called the radiation pressure.
But before we look at the EM Waves lets start with the famous equations which are source of them.
MAKING CONNECTIONS: RELATIVITY
Hearing all we do about Einstein, we sometimes get the impression that he invented relativity out of nothing. On the contrary, one of Einstein’s motivations was to solve difficulties in knowing how different observers see magnetic and electric fields.
END OF MODULE
Classical Electromagnetism is the unified FIELD framework to understand electricity, magnetism and the relationship between them. Classical Electromagnetism deals with electric charges and currents and their interactions via FIELDS as if all the quantities involved can be measured with unlimited precision. Here classical means simply "non-quantum". The quantum law w/ it's uncertainty and constant "h" is ignored.
Interestingly Maxwell's equations survived both the revolution of quantum physics and the development of Relativity of the early 20th century; neither of which has dimmed the luster of the electromagnetic field equations Maxwell wrote down 150 years ago. Why?
Well firstly, Maxwell's equations were ALREADY compatible with Relativity and needed no revision (unlike Newton's Law which faced major revisions). In fact Special relativity GREW out of Maxwell's equations, and Einstein himself was the first to admit it. Secondly, quantum modifications of the electromagnetic forces have turned out to be unimportant down to distances LESS THEN a picometer (10^-12 meters), which is 100 times smaller than an atom! That is, we can describe the repulsion and attraction of particles in the atom using the SAME LAWS that apply to electricity and magnets you are familiar with. Maxwell's equations govern them ALL!! However we DO need quantum mechanics to predict how these microscopic particles with BEHAVE under those forces. For distances smaller than 10^-12 we need QED (quantum electrodynamics), but it is really amazing to me HOW FAR REACHING Maxwell's equations are and how PRACTICAL they are!!
REVIEW & PREVIEW- Believe it or not, in Modules 2,4,5 & 6 we've already seen Maxwell's 4 equations, so this module we be a REVIEW.
But it will also be NEW in the sense of a New Mathematical Formalism to the same principles we have explored plus TWO big new insights. One being Maxwell's Correction to Ampere's Law WHICH leads to electromagnetic waves. In fact Maxwell's correction WAS A REQUIREMENT for electromagnetic waves to exist, so it was a HUGE discovery.
4)
When electric and magnetic FIELDS do not vary with time we can analyze them independent of one another which is mainly what we have done in this course UP TO Module #6 on Faraday's law. However when Electric and Magnetic FIELDS DO vary with time, they are interrelated by Maxwell's Equation and can give rise to electromagnetic waves as we'll see.
Where there is a force, there is energy. The energy corresponding to an EM force is called EM energy or radiation. This energy is transferred from one point in space to another through what are called EM waves.
Light
An electromagnetic wave carries energy and momentum.
The average power per unit area is called the intensity of the wave.
The momentum per unit time (that is, force) per unit area is called the radiation pressure.
But before we look at the EM Waves lets start with the famous equations which are source of them.
MAKING CONNECTIONS: RELATIVITY
Hearing all we do about Einstein, we sometimes get the impression that he invented relativity out of nothing. On the contrary, one of Einstein’s motivations was to solve difficulties in knowing how different observers see magnetic and electric fields.
END OF MODULE
Classical Electromagnetism is the unified FIELD framework to understand electricity, magnetism and the relationship between them. Classical Electromagnetism deals with electric charges and currents and their interactions via FIELDS as if all the quantities involved can be measured with unlimited precision. Here classical means simply "non-quantum". The quantum law w/ it's uncertainty and constant "h" is ignored.
Interestingly Maxwell's equations survived both the revolution of quantum physics and the development of Relativity of the early 20th century; neither of which has dimmed the luster of the electromagnetic field equations Maxwell wrote down 150 years ago. Why?
Well firstly, Maxwell's equations were ALREADY compatible with Relativity and needed no revision (unlike Newton's Law which faced major revisions). In fact Special relativity GREW out of Maxwell's equations, and Einstein himself was the first to admit it. Secondly, quantum modifications of the electromagnetic forces have turned out to be unimportant down to distances LESS THEN a picometer (10^-12 meters), which is 100 times smaller than an atom! That is, we can describe the repulsion and attraction of particles in the atom using the SAME LAWS that apply to electricity and magnets you are familiar with. Maxwell's equations govern them ALL!! However we DO need quantum mechanics to predict how these microscopic particles with BEHAVE under those forces. For distances smaller than 10^-12 we need QED (quantum electrodynamics), but it is really amazing to me HOW FAR REACHING Maxwell's equations are and how PRACTICAL they are!!
REVIEW & PREVIEW- Believe it or not, in Modules 2,4,5 & 6 we've already seen Maxwell's 4 equations, so this module we be a REVIEW.
But it will also be NEW in the sense of a New Mathematical Formalism to the same principles we have explored plus TWO big new insights. One being Maxwell's Correction to Ampere's Law WHICH leads to electromagnetic waves. In fact Maxwell's correction WAS A REQUIREMENT for electromagnetic waves to exist, so it was a HUGE discovery.
4)
When electric and magnetic FIELDS do not vary with time we can analyze them independent of one another which is mainly what we have done in this course UP TO Module #6 on Faraday's law. However when Electric and Magnetic FIELDS DO vary with time, they are interrelated by Maxwell's Equation and can give rise to electromagnetic waves as we'll see.

In the early nineteenth century, when electric and magnetic forces were thought to be two different forces, the physical quantity charge was organized into two different units in electrostatic phenomena and in magnetic phenomenon resulting in two different physical dimensions.
To their surprise, physicists noticed that the ratio of these two different units had the unit of velocity and it was precisely the speed of light! At the time no one could explain this.
James Clerk Maxwell put all this together when in 1865 he showed that an EM disturbance (wave) would propagate in space at the speed of light, and hence LIGHT was a wave (classically) and was electromagnetic in nature. Maxwell realized the basic principles of electromagnetism can be expressed in terms of four equations which display the mutual interaction between electric and magnetic fields.
To their surprise, physicists noticed that the ratio of these two different units had the unit of velocity and it was precisely the speed of light! At the time no one could explain this.
James Clerk Maxwell put all this together when in 1865 he showed that an EM disturbance (wave) would propagate in space at the speed of light, and hence LIGHT was a wave (classically) and was electromagnetic in nature. Maxwell realized the basic principles of electromagnetism can be expressed in terms of four equations which display the mutual interaction between electric and magnetic fields.

Maxwell's equations really show how ALL charged particles in the Universe (stationary or moving) produce FIELDS (electric and magnetic)!!
The Lorenz Force Law reciprocally tells you how FIELDS (waves) affect charges (particles)!
So mark this day as a very special day, as perhaps this is the first time you can truly appreciate Maxwell's Equations!! Here they are...
The Lorenz Force Law reciprocally tells you how FIELDS (waves) affect charges (particles)!
So mark this day as a very special day, as perhaps this is the first time you can truly appreciate Maxwell's Equations!! Here they are...
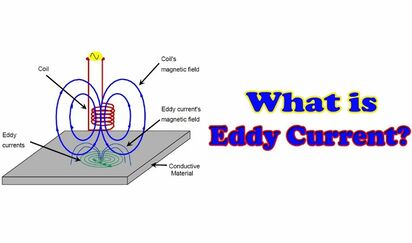
NOTE: Induced Electric Fields are very weak compared to electric fields directly from charges.
Because of this, in PEMF devices that DO use electrically neutral, current carrying wires (most do), the changing MAGNETIC field AND it's corresponding induced Eddy currents (EMF) dominates the PEMF therapy (which is what we want for optimal penetration and healing).
But if the changing Magnetic field is TOO Strong it CAN produce Eddy Currents that are damaging to the body.
Because of this, in PEMF devices that DO use electrically neutral, current carrying wires (most do), the changing MAGNETIC field AND it's corresponding induced Eddy currents (EMF) dominates the PEMF therapy (which is what we want for optimal penetration and healing).
But if the changing Magnetic field is TOO Strong it CAN produce Eddy Currents that are damaging to the body.

High intensity is like a stage 1-5 hurricane depending on the frequency and intensities (both higher frequency AND higher intensity INCREASE the Eddy Current's Intensity just as Air/Land/Sea Temperature and Atmospheric Pressure influence a Hurricane.
Hurricane Conditions That Make Hurricanes More Dangerous
PEMF Conditions That Make PEMF Devices more Dangerous (all these INCREASE Eddy Currents
Hurricane Conditions That Make Hurricanes More Dangerous
- low air pressure.
- warm temperatures.
- moist ocean air.
- tropical winds (near the equator).
PEMF Conditions That Make PEMF Devices more Dangerous (all these INCREASE Eddy Currents
- High Intensity
- Larger Coil Size
- Higher Frequency
- Rapid Rise and Fall (Ringer) Waveform
Differential Form of Maxwell's Equations (Optional)

Differential Form of Maxwell's Equations
Lets Take a stab at understanding the geometric principles of the differential form of Maxwell's Equations which are the most powerful expression, though both in theory can give the same results.
It is ok if you cannot follow all the math, just try to get a basic grasp of the concepts.
The main 3 concepts we need to introduce are the Nabla Operator, Divergence and Curl.
Lets Take a stab at understanding the geometric principles of the differential form of Maxwell's Equations which are the most powerful expression, though both in theory can give the same results.
It is ok if you cannot follow all the math, just try to get a basic grasp of the concepts.
The main 3 concepts we need to introduce are the Nabla Operator, Divergence and Curl.
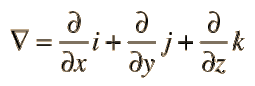
Nabla - the del Operator
The inverted uppercase delta appears in the differential form of all four of Maxwell's equations. This symbol represents a vector differential operator called Nabla or Del, and it's presence instructs you to take derivatives of the quantity on which the operator is acting. Derivatives in general tell you the rate of change of something.
The exact form of these derivatives depends on the symbol following the del operator with del "dot" representing divergence (first two Maxwell equations), and del "cross" representing curl (second two equations).
Don't worry if you have not had calculus, I will try to give visual explanations of how these operators work.
The inverted uppercase delta appears in the differential form of all four of Maxwell's equations. This symbol represents a vector differential operator called Nabla or Del, and it's presence instructs you to take derivatives of the quantity on which the operator is acting. Derivatives in general tell you the rate of change of something.
The exact form of these derivatives depends on the symbol following the del operator with del "dot" representing divergence (first two Maxwell equations), and del "cross" representing curl (second two equations).
Don't worry if you have not had calculus, I will try to give visual explanations of how these operators work.

Flux and Divergence - 1st two Maxwells (Gauss's Law for Electricity and Magnetism)
The First 2 Maxwell equations how radiating electric fields and magnetic fields created.
Flux, integrate the total electric or magnetic field over a surface. Sum total of each little area. DA
Divergence is well chosen for it is a measure of how much the field spreads out from a point in question. Positive divergence flows OUT like a faucet/source, while negative divergence flows IN like a drain/sink. The divergence at any point is a measure of the tendency of the flow vectors to diverge from that point (that is, to carry more material away from it than is brought in).
Both Flux and Divergence deal with the "flow" of a vector field, but with an important difference. Flux is defined over an area, while divergence applies to individual points.
The First 2 Maxwell equations how radiating electric fields and magnetic fields created.
Flux, integrate the total electric or magnetic field over a surface. Sum total of each little area. DA
Divergence is well chosen for it is a measure of how much the field spreads out from a point in question. Positive divergence flows OUT like a faucet/source, while negative divergence flows IN like a drain/sink. The divergence at any point is a measure of the tendency of the flow vectors to diverge from that point (that is, to carry more material away from it than is brought in).
Both Flux and Divergence deal with the "flow" of a vector field, but with an important difference. Flux is defined over an area, while divergence applies to individual points.
Points of positive divergence are sources (like faucets in fluid analogy, and positive charges in electrostatics).
Points of negative divergence are sinks (drains in fluid flow, and negative charges in electrostatics).
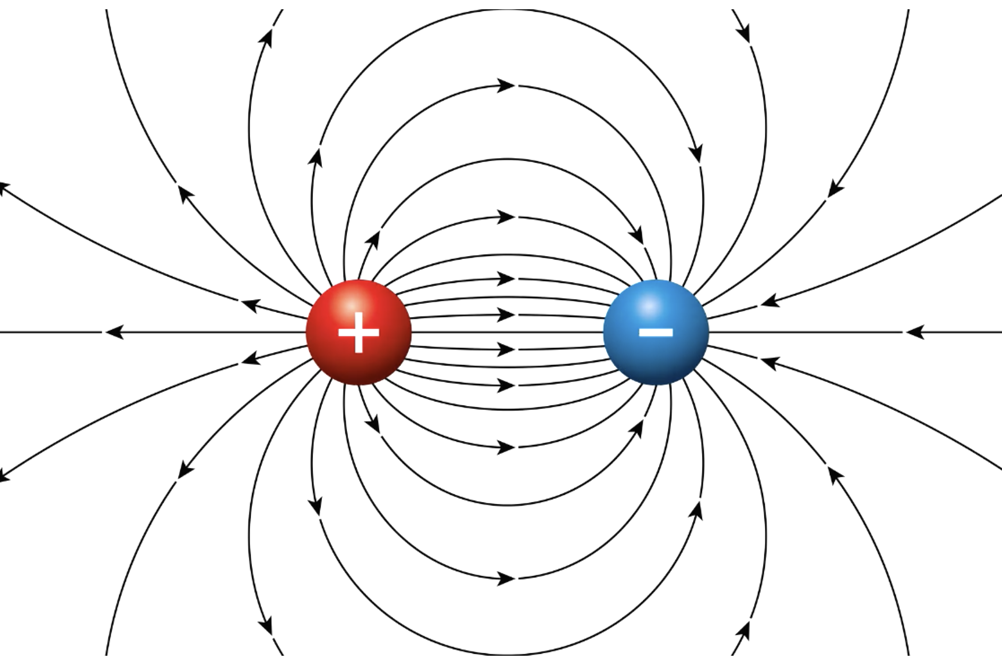
+ positive Electric charge is the Source for the electric field - Field Lines Flow out
- negative Electric charge is the Sink for the electric field - Field Lines Flow IN
Note: there are NO magnetic monopoles or SOURCE charges for the magnetic field which is why the second equation is = 0.
Divergence is PARTICLE - LIKE
Divergence is a vector operator that produces a scalar field, giving the quantity of a vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.
As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value.
Points of negative divergence are sinks (drains in fluid flow, and negative charges in electrostatics).
+ positive Electric charge is the Source for the electric field - Field Lines Flow out
- negative Electric charge is the Sink for the electric field - Field Lines Flow IN
Note: there are NO magnetic monopoles or SOURCE charges for the magnetic field which is why the second equation is = 0.
Divergence is PARTICLE - LIKE
Divergence is a vector operator that produces a scalar field, giving the quantity of a vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.
As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value.
Points of positive divergence are sources (like faucets in fluid analogy, and positive charges in electrostatics).
Points of negative divergence are sinks (drains in fluid flow, and negative charges in electrostatics).
+ positive Electric charge is the Source for the electric field - Field Lines Flow out
- negative Electric charge is the Sink for the electric field - Field Lines Flow IN
Points of negative divergence are sinks (drains in fluid flow, and negative charges in electrostatics).
+ positive Electric charge is the Source for the electric field - Field Lines Flow out
- negative Electric charge is the Sink for the electric field - Field Lines Flow IN
Gauss's Law for Electric Fields

The Differential form of Gauss's Law states:
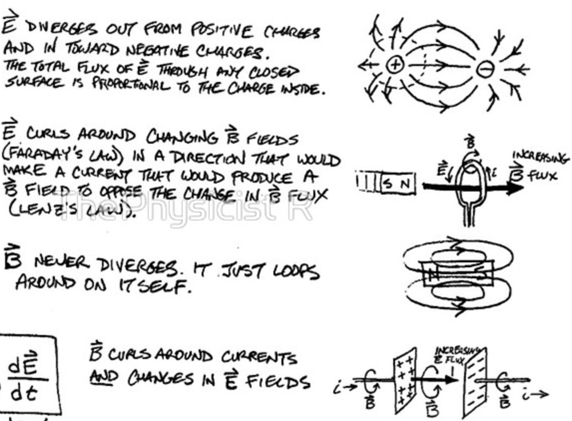
The electric field produced by electric charge diverges from positive charges and converges from negative charges.
The electric field produced by electric charge diverges from positive charges and converges from negative charges.
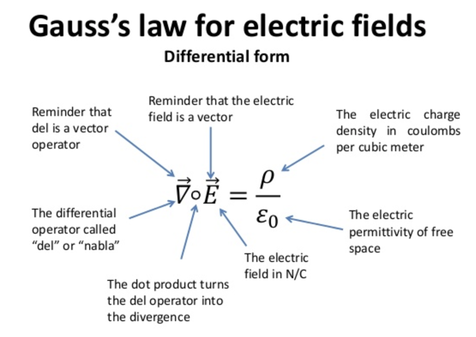
The First Equation is Again Gauss's Law for Electric Charge but in differential form it represents the divergence of the electric field at each point in space.
In a nutshell, The First Equation is Gauss's Law which tells you charges emit or absorb electric field lines or flux depending on their magnitude and sign. That is, Electric field lines originate or flow out of positive charges and terminate or flow into negative charges. The electric field is defined as the force per unit charge on a test charge, and the strength of the force is related to the electric constant ε0, also known as the permittivity of free space.
Points of positive divergence are sources (like faucets in fluid analogy, and positive charges in electrostatics).
Points of negative divergence are sinks (drains in fluid flow, and negative charges in electrostatics).
+ positive Electric charge is the Source for the electric field - Field Lines Flow out
- negative Electric charge is the Sink for the electric field - Field Lines Flow IN
In a nutshell, The First Equation is Gauss's Law which tells you charges emit or absorb electric field lines or flux depending on their magnitude and sign. That is, Electric field lines originate or flow out of positive charges and terminate or flow into negative charges. The electric field is defined as the force per unit charge on a test charge, and the strength of the force is related to the electric constant ε0, also known as the permittivity of free space.
Points of positive divergence are sources (like faucets in fluid analogy, and positive charges in electrostatics).
Points of negative divergence are sinks (drains in fluid flow, and negative charges in electrostatics).
+ positive Electric charge is the Source for the electric field - Field Lines Flow out
- negative Electric charge is the Sink for the electric field - Field Lines Flow IN
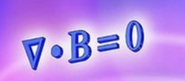
The Differential form of Gauss's Law For Magnetic Fields states:
The divergence of the magnetic field at any point is zero.
Maxwell's Second differential equation is straightforward because there ARE no magnetic monopoles, that is there are no point sources for the magnetic field. Magnetic field North and South poles always come together to form a closed loop. There is no such thing as an isolated North or South pole like there is a positive and negative charge. This is one of the main reasons, as we mentioned that magnetic fields penetrate more deeply than light, electric currents and electric fields, because the North-South pole magnetic fields formed closed loops and they most close back on themselves, even if there is Lead in the way.
Another way of say this is the total magnetic flux through any closed surface is zero. That is (again) because there are no source "faucets" for the magnetic field (or "sinks") using the fluid flow analogy.
The divergence of the magnetic field at any point is zero.
Maxwell's Second differential equation is straightforward because there ARE no magnetic monopoles, that is there are no point sources for the magnetic field. Magnetic field North and South poles always come together to form a closed loop. There is no such thing as an isolated North or South pole like there is a positive and negative charge. This is one of the main reasons, as we mentioned that magnetic fields penetrate more deeply than light, electric currents and electric fields, because the North-South pole magnetic fields formed closed loops and they most close back on themselves, even if there is Lead in the way.
Another way of say this is the total magnetic flux through any closed surface is zero. That is (again) because there are no source "faucets" for the magnetic field (or "sinks") using the fluid flow analogy.
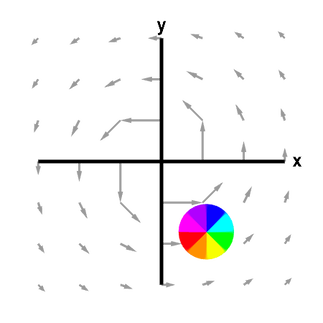
Curl - 2nd Two Maxwells (Faradays Law of Induction and Ampere's law of Current Flow)
Last Two equations how circulating electric and magnetic fields are created.
AND how changing electric and magnetic fields create each other (leads to EM waves)
The name curl is ALSO well chosen, for it is a measure of how much a field curls, swirls, rotates or twists around the point in question - much like divergence is a measure of the tendency of the field to flow away from a point. Use the right hand rule for detecting POSITIVE curl (counterclockwise) and negative curl (counterclockwise).
Last Two equations how circulating electric and magnetic fields are created.
AND how changing electric and magnetic fields create each other (leads to EM waves)
The name curl is ALSO well chosen, for it is a measure of how much a field curls, swirls, rotates or twists around the point in question - much like divergence is a measure of the tendency of the field to flow away from a point. Use the right hand rule for detecting POSITIVE curl (counterclockwise) and negative curl (counterclockwise).

CURL IS WAVELIKE, No beginning and no end, tendency of fields to loop back on themselves in complete circles.
In vector calculus, the curl is a vector operator that describes the infinitesimal rotation of a vector field in three-dimensional Euclidean space. At every point in the field, the curl of that point is represented by a vector. The attributes of this vector (length and direction) characterize the rotation at that point.
The direction of the curl is the axis of rotation, as determined by the right-hand rule, and the magnitude of the curl is the magnitude of rotation. If the vector field represents the flow velocity of a moving fluid, then the curl is the circulation density of the fluid. A vector field whose curl is zero is called irrotational.
Note: vector field with zero divergence everywhere is called incompressible or solenoidal – in which case any closed surface has no net flow across it.
In vector calculus, the curl is a vector operator that describes the infinitesimal rotation of a vector field in three-dimensional Euclidean space. At every point in the field, the curl of that point is represented by a vector. The attributes of this vector (length and direction) characterize the rotation at that point.
The direction of the curl is the axis of rotation, as determined by the right-hand rule, and the magnitude of the curl is the magnitude of rotation. If the vector field represents the flow velocity of a moving fluid, then the curl is the circulation density of the fluid. A vector field whose curl is zero is called irrotational.
Note: vector field with zero divergence everywhere is called incompressible or solenoidal – in which case any closed surface has no net flow across it.
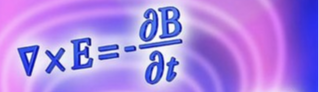
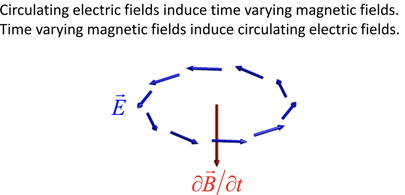
Faraday's Law in Differential Form States:
A circulating Electric Field is produced by a magnetic induction that changes with time.
Lenz's Law: Currents induced by changing magnetic flux always flow in the direction so as to oppose the change in flux.
A circulating Electric Field is produced by a magnetic induction that changes with time.
Lenz's Law: Currents induced by changing magnetic flux always flow in the direction so as to oppose the change in flux.
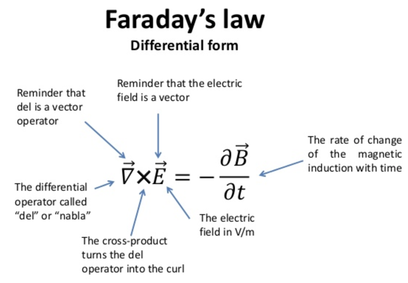
Faraday's Law in Differential Form
The third equation is Faradays law of of EM induction which shows how a magnetic field that changes with time (time varying) produces or generates a CIRCULATING electric field.
The left side of the equation is a mathematical description of the curl of the electric field - the tendency of field lines to circulate around a point. The right side represents the rate of change of the magnetic field over time.
The Electric Field Curls around a Changing Magnetic Field in a direction that would make a current that would produce a Magnetic Field to Oppose the change in Magnetic Flux (Lenz's Law).
The third equation is Faradays law of of EM induction which shows how a magnetic field that changes with time (time varying) produces or generates a CIRCULATING electric field.
The left side of the equation is a mathematical description of the curl of the electric field - the tendency of field lines to circulate around a point. The right side represents the rate of change of the magnetic field over time.
The Electric Field Curls around a Changing Magnetic Field in a direction that would make a current that would produce a Magnetic Field to Oppose the change in Magnetic Flux (Lenz's Law).

Circulation - 2nd Two Maxwells (Faradays Law of Induction and Ampere's law of Current Flow)
Circulation: Integrate the magnetic or electric field around a closed loop. This is the summed total of each little magnetic or electric field point around a loop that is circulating. DS.
So the electric field does not radiate outward in straight lines with a 1/r^2 dropoff, rather, it curls, swirls, rotates or twists around the point in question.
Circulation: Integrate the magnetic or electric field around a closed loop. This is the summed total of each little magnetic or electric field point around a loop that is circulating. DS.
So the electric field does not radiate outward in straight lines with a 1/r^2 dropoff, rather, it curls, swirls, rotates or twists around the point in question.
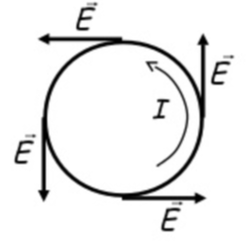
Now lets look at the Geometry of the Induced Electric Fields Produced by Changing Magnetic Fields as it is different than static charges.
In a nutshell electric charges create radiating electric fields where the electric fields radiates out from positive charges (source/faucet) and into negative charges (sink/drain).
By contrast changing magnetic fields create Circulating Electric Fields which form closed loops with no source charges and no beginning or end. These circulating electric fields are the force that drives Eddy currents as we showed earlier.
In a nutshell electric charges create radiating electric fields where the electric fields radiates out from positive charges (source/faucet) and into negative charges (sink/drain).
By contrast changing magnetic fields create Circulating Electric Fields which form closed loops with no source charges and no beginning or end. These circulating electric fields are the force that drives Eddy currents as we showed earlier.
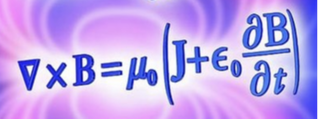
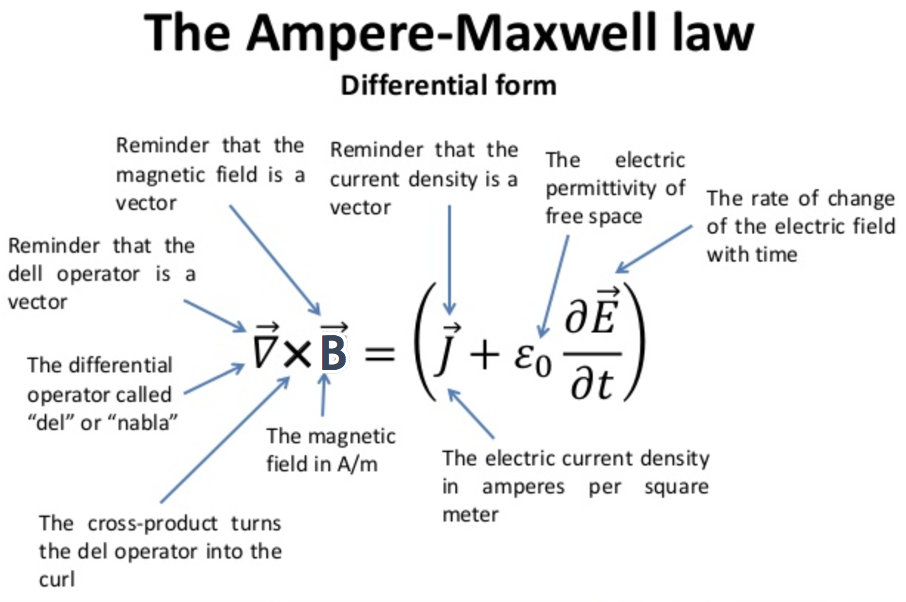
The Ampere-Maxwell Law in Differential Form States:
The Circulating Magnetic Field is produced by any electric current and by an electric field that changes with time.
And the 4th and last Maxwell equation expresses Amperes law by showing how an electric current can generate a magnetic field as we talked about earlier
PLUS there is second and NEW term in the equation was added by Maxwell (not in Ampere's original equation) in analogy with Faradays law, to account for the fact that a time varying electric field also generates a circulating magnetic field....
The Circulating Magnetic Field is produced by any electric current and by an electric field that changes with time.
And the 4th and last Maxwell equation expresses Amperes law by showing how an electric current can generate a magnetic field as we talked about earlier
PLUS there is second and NEW term in the equation was added by Maxwell (not in Ampere's original equation) in analogy with Faradays law, to account for the fact that a time varying electric field also generates a circulating magnetic field....
Displacement current is Electric Induction symmetric mathematically in its effects to magnetic induction. The reason many decades went by before Maxwell figured it out, is that the magnetic fields induced by the changing electric flux are extremely weak and therefore difficult to measure.
The key concept here is that a changing electric field produces a changing magnetic field even though no charges are present and no physicals currents flow. Through this mechanism, electromagnetic waves (as we'll see) may propagate through even a perfect vacuum, as a changing magnetic fields induce electric fields and changing electric fields induce magnetic fields. Maxwell's displacement current or electric induction is what makes light possible!!!
The key concept here is that a changing electric field produces a changing magnetic field even though no charges are present and no physicals currents flow. Through this mechanism, electromagnetic waves (as we'll see) may propagate through even a perfect vacuum, as a changing magnetic fields induce electric fields and changing electric fields induce magnetic fields. Maxwell's displacement current or electric induction is what makes light possible!!!
SUMMARY : An electric charge produces an electric field flux or flow that radiates away from a positive charge (like image here) or towards a negative charge. Like a source/faucet or sink/drain. Magnetic fields by contrast curl and swirl or circulate around moving charges like steady currents. See image here. The direction of the circulation is governed by the right hand rule.
Electric fields radiate away or towards charges while magnetic fields swirl or circulate around currents. These equations define the Electric or Magnetic field at each point in space around a source charge or current. And remember these are vector fields such that the electric and magnetic fields are vectors at each point. Kinda like wind velocity or water flow... Again use the water flow analogy to help see this.
Electric fields radiate away or towards charges while magnetic fields swirl or circulate around currents. These equations define the Electric or Magnetic field at each point in space around a source charge or current. And remember these are vector fields such that the electric and magnetic fields are vectors at each point. Kinda like wind velocity or water flow... Again use the water flow analogy to help see this.
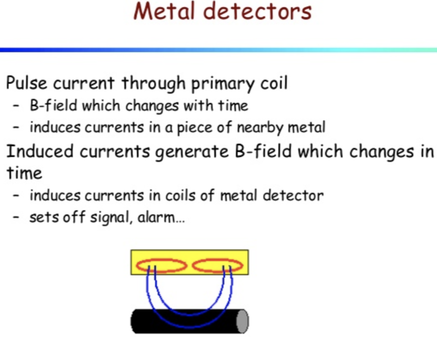
How Metal detectors Work.
And it is for this reason why I tell people that it is not ideal to wear a lot of metal OR lay your pemf mat on a metal table OR sit in a metal chair while using a pemf device.
It is because induced currents develop in the metal objects (due to free electrons) which in turn generate a B-field that will slightly interfere with PEMF field.
Having said that a small amount of metal (wedding band, zipper, button, earring, etc.) is not a big deal as it produces negligible eddy currents.
And it is for this reason why I tell people that it is not ideal to wear a lot of metal OR lay your pemf mat on a metal table OR sit in a metal chair while using a pemf device.
It is because induced currents develop in the metal objects (due to free electrons) which in turn generate a B-field that will slightly interfere with PEMF field.
Having said that a small amount of metal (wedding band, zipper, button, earring, etc.) is not a big deal as it produces negligible eddy currents.
Braking using eddy currents is safer because factors such as rain do not affect the braking and the braking is smoother. However, eddy currents cannot bring the motion to a complete stop, since the force produced decreases with speed. Thus, speed can be reduced from say 20 m/s to 5 m/s, but another form of braking is needed to completely stop the vehicle.
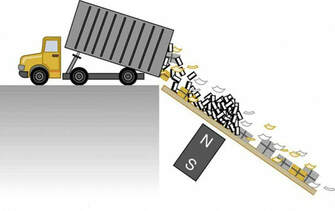
Since eddy currents and magnetic damping occur only in conductors, recycling centers can use magnets to separate metals from other materials. Trash is dumped in batches down a ramp, beneath which lies a powerful magnet. Conductors in the trash are slowed by magnetic damping while nonmetals in the trash move on, separating from the metals. This works for all metals, not just ferromagnetic ones. A magnet can separate out the ferromagnetic materials alone by acting on stationary trash.

Other major applications of eddy currents are in metal detectors and braking systems in trains and roller coasters. Portable metal detectors consist of a primary coil carrying an alternating current and a secondary coil in which a current is induced. An eddy current will be induced in a piece of metal close to the detector which will cause a change in the induced current within the secondary coil, leading to some sort of signal like a shrill noise.
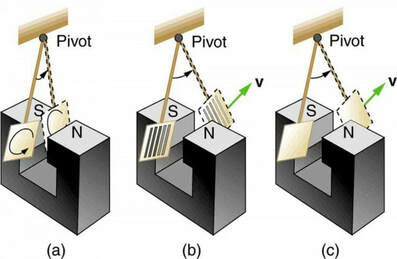
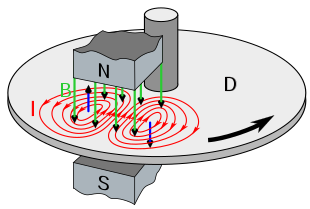
Eddy Currents and Magnetic Damping
Eddy currents can produce significant drag, called magnetic damping, on the motion involved. Consider the apparatus shown in This Figure, which swings a pendulum bob between the poles of a strong magnet. (This is another favorite physics lab activity.) If the bob is metal, there is significant drag on the bob as it enters and leaves the field, quickly damping the motion. If, however, the bob is a slotted metal plate, as shown in (b) there is a much smaller effect due to the magnet.
Eddy currents can produce significant drag, called magnetic damping, on the motion involved. Consider the apparatus shown in This Figure, which swings a pendulum bob between the poles of a strong magnet. (This is another favorite physics lab activity.) If the bob is metal, there is significant drag on the bob as it enters and leaves the field, quickly damping the motion. If, however, the bob is a slotted metal plate, as shown in (b) there is a much smaller effect due to the magnet.
The classical model of electricity and magnetism makes use of the ideas of electric and magnetic fields. Maxwell’s equations describe how these fields behave, and the Lorentz force equation, which describes how the fields push and pull charged particles and magnets.
A prediction of Maxwell’s equations is that there are waves in the electromagnetic field which travel at the speed of light. These waves were identified with light by the experiments of Hertz and others.
A prediction of Maxwell’s equations is that there are waves in the electromagnetic field which travel at the speed of light. These waves were identified with light by the experiments of Hertz and others.

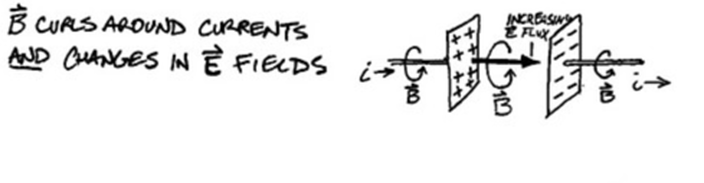
In order to make this equation work for all possible electromagnetic scenarios, Maxwell needed to consider a situation where a magnetic field is induced, but not from the flow of current.
For example, picture a charged capacitor that's connected to wires on both sides.
As the capacitor discharges, current runs through both wires, generating a changing magnetic flux, just like Ampere's Law says.
But a changing magnetic flux is also induced between the two plates when there's no wire connecting the plates.
For example, picture a charged capacitor that's connected to wires on both sides.
As the capacitor discharges, current runs through both wires, generating a changing magnetic flux, just like Ampere's Law says.
But a changing magnetic flux is also induced between the two plates when there's no wire connecting the plates.