Picturing Chaos as Order - Strange Attractors
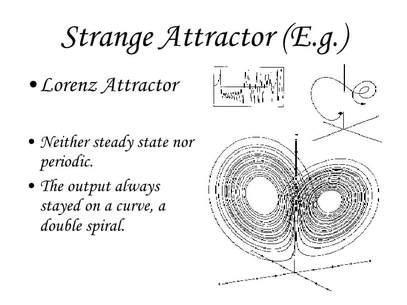
We have been focusing on the unpredictablity in Chaos.
But Chaos is Yang as well as yin, order as well as randomness
Strange Attractor is a way to visualize chaos
Circle is a shape to symbolize periodicity. Coming back on itself.
Strange attractors are the shape of chaos.
It's strange because it's geometry is strange. It is infinitely complex
It's an attractor because it attracts the system that it represents like it is attracted to it.
Reveals unexpected order in chaos, means it is partially predictable and controllable.
Cardiac arrhtyhmias and lasers.
Meterologist Ed Lorenz of MIT.
Could chaos result in simpler systems
Convection. Rotating flow of fluid. Pattern of convection sets in when warm air rises up
and cools as it gets higher. Because it is denser it starts to descend and sink again.
Tabletop waterwheel. Malkus waterwheel.
Water is pumped up and sprayed out.
Adjust the amount of friction...
1) When the break is set to be tight, the wheel sets into a uniform rotation.
Simple steady rotation is the attractor. POINT
2) If the break is loose, then it rocks back and forth, settles into its attractor.
Attractor CIRCLE
3) If set the break in intermediate amount of friction, than it rotates erratically.
STRANGE ATTRACTOR
Same as Lorenz's convection model.
Used poincares state space
State is amount of information needed to predict the future of a system, using the laws of motion.
Collection of variables needed to say what a system will do in the next instant. And instant by instant you can predict forward into the forward.
1) Spin Rate
2) gravitational torque
3) level of top-heaviness
You can think of it as three variables
State space has 3 dimensions, one dimension for each variable.
Using computer simulation graph state space.
Like a comet sailing through space, except this is a comet sailing through abstract state space.
Abstract comet moving around relates to actual waterwheel.
But Chaos is Yang as well as yin, order as well as randomness
Strange Attractor is a way to visualize chaos
Circle is a shape to symbolize periodicity. Coming back on itself.
Strange attractors are the shape of chaos.
It's strange because it's geometry is strange. It is infinitely complex
It's an attractor because it attracts the system that it represents like it is attracted to it.
Reveals unexpected order in chaos, means it is partially predictable and controllable.
Cardiac arrhtyhmias and lasers.
Meterologist Ed Lorenz of MIT.
Could chaos result in simpler systems
Convection. Rotating flow of fluid. Pattern of convection sets in when warm air rises up
and cools as it gets higher. Because it is denser it starts to descend and sink again.
Tabletop waterwheel. Malkus waterwheel.
Water is pumped up and sprayed out.
Adjust the amount of friction...
1) When the break is set to be tight, the wheel sets into a uniform rotation.
Simple steady rotation is the attractor. POINT
2) If the break is loose, then it rocks back and forth, settles into its attractor.
Attractor CIRCLE
3) If set the break in intermediate amount of friction, than it rotates erratically.
STRANGE ATTRACTOR
Same as Lorenz's convection model.
Used poincares state space
State is amount of information needed to predict the future of a system, using the laws of motion.
Collection of variables needed to say what a system will do in the next instant. And instant by instant you can predict forward into the forward.
1) Spin Rate
2) gravitational torque
3) level of top-heaviness
You can think of it as three variables
State space has 3 dimensions, one dimension for each variable.
Using computer simulation graph state space.
Like a comet sailing through space, except this is a comet sailing through abstract state space.
Abstract comet moving around relates to actual waterwheel.
Attractors
1) When the break is set to be tight, the wheel sets into a uniform rotation.
Transient behavior than it spirals into to a point.
Constant amount of top-heaviness and spin.
damped oscillation into uniform motion or steady and constant rotation.
Attractor - Represents a systems natural long-term mode of behavior.
If the system is nudged off its attractor by disturbing it slightly in some way, it will soon head back.
System determined to get back to attractor.
Relax back to attractor,
Someone startles you and heart rate goes up, settles back to attractor.
Your heart like many systems in nature, is carefully regulated to keep it within certain limits,
Unchanging steady state is a point. Equilibrium. Stays in SAME state until perturbed.
2) If the break is loose, then it rocks back and forth, settles into its attractor.
Attractor CIRCLE
Attracting CYCLE as it oscillates and returns to itself.
System settles unto a loop.
Lorenz trying to visualize an attractor on a chaotic state. Not even Poincare did that.
3) If set the break in intermediate amount of friction, than it rotates erratically.
STRANGE ATTRACTOR
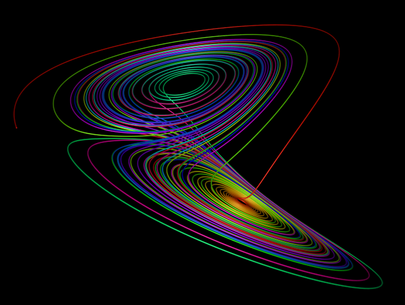
Twist out of the twilight zone. Strange attractor for Lorenz Attractor looks like a pair of butterfly wings.
Makes a few loops on each side of wing, then the it goes back.
Pair of surfaces joined together at a hinge.
These surfaces cannot join at a hinge.
If the two
two different paths leading to same point. Impossible
Past cannot go running back into two futures. Unique past and future.
They must be coming close but barely missing.
Sheets of mica
There are 2 then 4 , then 8, then 16...
There must be an infinite complex of surfaces.
Strange Wings made of an infinite number of Surfaces
Think of a parking garage... Many levels like many sheets.
Instead of two wings, two towers.
You get wipped around from one side to the other without repearing
Transient behavior than it spirals into to a point.
Constant amount of top-heaviness and spin.
damped oscillation into uniform motion or steady and constant rotation.
Attractor - Represents a systems natural long-term mode of behavior.
If the system is nudged off its attractor by disturbing it slightly in some way, it will soon head back.
System determined to get back to attractor.
Relax back to attractor,
Someone startles you and heart rate goes up, settles back to attractor.
Your heart like many systems in nature, is carefully regulated to keep it within certain limits,
Unchanging steady state is a point. Equilibrium. Stays in SAME state until perturbed.
2) If the break is loose, then it rocks back and forth, settles into its attractor.
Attractor CIRCLE
Attracting CYCLE as it oscillates and returns to itself.
System settles unto a loop.
Lorenz trying to visualize an attractor on a chaotic state. Not even Poincare did that.
3) If set the break in intermediate amount of friction, than it rotates erratically.
STRANGE ATTRACTOR
Twist out of the twilight zone. Strange attractor for Lorenz Attractor looks like a pair of butterfly wings.
Makes a few loops on each side of wing, then the it goes back.
Pair of surfaces joined together at a hinge.
These surfaces cannot join at a hinge.
If the two
two different paths leading to same point. Impossible
Past cannot go running back into two futures. Unique past and future.
They must be coming close but barely missing.
Sheets of mica
There are 2 then 4 , then 8, then 16...
There must be an infinite complex of surfaces.
Strange Wings made of an infinite number of Surfaces
Think of a parking garage... Many levels like many sheets.
Instead of two wings, two towers.
You get wipped around from one side to the other without repearing
Strange Attractor

Strange Attractor
1) Determinism of the Motion - no choice as to future (differential equation). Towing appartatus
2) Non periodic, you never come back to your initial state.
3) Confined to the strange attractor - cannot leave the parking garage.
4) Extreme sensitivity to initial conditions... No matter how close your friend starts to you, you may stay together for a while by soon you will have totally different fates.
Why are strange attractors so important.
Chaos is not the absent of order,
It is a marvelous subtle state that is poised between order on the one hand and randomness on the other.
With both aspects intermingled.
Butterfly pattern does not emerge right away, it takes time, a cumulative order.
Yet there is a randomness... Tiny differences grow expontentially making it impossible to forecast or predict what this system will do far into the future.
Confusing interplay of order and randomness CHAOS is NOT randomness.
Chaos = Order + Randomness.
Look at chaos in time instead of state space.
Use chaos and harness its properties
Epilepsy
Arrthymias
Space travel
Communications technology - encryption
1) Determinism of the Motion - no choice as to future (differential equation). Towing appartatus
2) Non periodic, you never come back to your initial state.
3) Confined to the strange attractor - cannot leave the parking garage.
4) Extreme sensitivity to initial conditions... No matter how close your friend starts to you, you may stay together for a while by soon you will have totally different fates.
Why are strange attractors so important.
Chaos is not the absent of order,
It is a marvelous subtle state that is poised between order on the one hand and randomness on the other.
With both aspects intermingled.
Butterfly pattern does not emerge right away, it takes time, a cumulative order.
Yet there is a randomness... Tiny differences grow expontentially making it impossible to forecast or predict what this system will do far into the future.
Confusing interplay of order and randomness CHAOS is NOT randomness.
Chaos = Order + Randomness.
Look at chaos in time instead of state space.
Use chaos and harness its properties
Epilepsy
Arrthymias
Space travel
Communications technology - encryption
Iterated Maps - Another kind of Order in Chaos
1) Differential Equations - Newtons
2) Strange Attractors - Lorenz
3) Iterated Maps -
These 3 all all kinds of photography. The distinction between them is how they handle time.
Suppose we wanted to film a modern dancer (represents a chaotic system).
How do we capture the motion of this dancer?
1) First we could simply just record a video of the dancer. Movie Camera - Time flows continuous, though frame by frame, lets assume a time interval between frames (epsilon). DIFFERENTIAL EQUATION - the logic behind the movie. Which frame should follow. Let's you see how a system is going to unfold, instant by instant and frame by frame. most information you can have. TOO MUCH information.
Strange Attractors and Iterated maps are two ways of boiling down differential equations into something simpler.
2) Time Lapsed Photograph - capture all the movements in one image.
Instead of being filmed continuously, all times are shown at once, superimposed.
STRANGE ATTRACTOR - abstract time lapsed photo in state space.
Long term cumulative effects of chaos... Like shutter opening in stars move in circles around North star.
Concentric circles, simple beautiful order
Lorenz saw much more complex... Not perfect circles, or a tangled mess.. but pair of butterfly wings.
Stars, dancer dancing...
3) Turn off the lights and flash a strob light. The dance has a jerky feel to it.
Discrete Time instead of continuous. ITERATED MAP.. Flash a strob light
2) Strange Attractors - Lorenz
3) Iterated Maps -
These 3 all all kinds of photography. The distinction between them is how they handle time.
Suppose we wanted to film a modern dancer (represents a chaotic system).
How do we capture the motion of this dancer?
1) First we could simply just record a video of the dancer. Movie Camera - Time flows continuous, though frame by frame, lets assume a time interval between frames (epsilon). DIFFERENTIAL EQUATION - the logic behind the movie. Which frame should follow. Let's you see how a system is going to unfold, instant by instant and frame by frame. most information you can have. TOO MUCH information.
Strange Attractors and Iterated maps are two ways of boiling down differential equations into something simpler.
2) Time Lapsed Photograph - capture all the movements in one image.
Instead of being filmed continuously, all times are shown at once, superimposed.
STRANGE ATTRACTOR - abstract time lapsed photo in state space.
Long term cumulative effects of chaos... Like shutter opening in stars move in circles around North star.
Concentric circles, simple beautiful order
Lorenz saw much more complex... Not perfect circles, or a tangled mess.. but pair of butterfly wings.
Stars, dancer dancing...
3) Turn off the lights and flash a strob light. The dance has a jerky feel to it.
Discrete Time instead of continuous. ITERATED MAP.. Flash a strob light
Iterated Maps
Find a rule that animates the map. jumps many frames... leap-frogging.
Sprint through time with iterated map. Map as a verb, not a noun.
Take something and mapping on to something else. Iterated mapping.
Mathematical machine.
The map is a machine that eats numbers and spits numbers out.
Takes you from one frame to the next.
Iterated because it takes the output number and feeds it back into the input
and goes around and around
Simple iterated map in lorenz system that drives the chaos in a leap frogging way.
Where the differential equation has us inch forward instant by instant, the iterated map
allows us to sprint.
Iterated Maps are Pivotal to Chaos, they orchestate chaos in many systems from electronics to animals population.
Chaotic time series Z.
Record only the PEAK values.
Just a peak in one snapshot, predict anything about the next peak.
Sacrifice a lot of information in between BUT it would allow us to leap frog and sprint quickly forward.
Can Zn predict anything about Zn+1
Need to repeat the process and iterate the map
Sprint through time with iterated map. Map as a verb, not a noun.
Take something and mapping on to something else. Iterated mapping.
Mathematical machine.
The map is a machine that eats numbers and spits numbers out.
Takes you from one frame to the next.
Iterated because it takes the output number and feeds it back into the input
and goes around and around
Simple iterated map in lorenz system that drives the chaos in a leap frogging way.
Where the differential equation has us inch forward instant by instant, the iterated map
allows us to sprint.
Iterated Maps are Pivotal to Chaos, they orchestate chaos in many systems from electronics to animals population.
Chaotic time series Z.
Record only the PEAK values.
Just a peak in one snapshot, predict anything about the next peak.
Sacrifice a lot of information in between BUT it would allow us to leap frog and sprint quickly forward.
Can Zn predict anything about Zn+1
Need to repeat the process and iterate the map
Lorenz Map (or graph of Lorenz map... map is a machine of function).
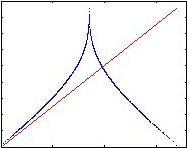
Make a Graph of Zn+1 vs Zn (y vs x).
Lorenz spirals spiral and get larger then shoot over to the other side.
Lorenz realized that Z measured the height of these growing spirals
When the spiral gets too high it seems to want to jump.. so it seemed that when Z exceed a certain value, the system would jump.
Maybe just knowing the maximum before a leap would predict the next top of the spiral.
Lorenz Map... How is a simple curve there?
How is chaos different than randomness.
If this system were random, than there would be a cloud of fuzz.
Probability theory... In a random system, whatever can happen, can happen next with some probability.
You would not see just one outcome you would see a whole scatter or buckshot of outcomes.
In a deterministic system in contrast to a random system, only ONE thing can happen next.
One one thing can happen next given.
A strob light flashes
Record value Z, integrate the differential equation until the next peak and then ZAP the light goes off.
And keep repeating. Strob light triggered when a maximum is reached.
Lorenz map on only works for a system when it is on its attractor.
But remember there are transient times that it takes for the system to reach the attractor.
Transient behavior is just an artifact of how we started it. Let that garbage sort itself out until on attractor.
Why is the Lorenz map so important? Becaue it is so simple.
Simply
Tell me a Zn, tell me the next Zn+1
Iterated map lightning fast and captures the heart of
Great boiling down of information in the differential equations (much less cumbersome).
The true laws of physics and chemistry and the laws of nature are expressed in differential equations.
Leave differential equations behind..
Exploration of iterated maps provide some of the biggest insights in Chaos.
Lorenz spirals spiral and get larger then shoot over to the other side.
Lorenz realized that Z measured the height of these growing spirals
When the spiral gets too high it seems to want to jump.. so it seemed that when Z exceed a certain value, the system would jump.
Maybe just knowing the maximum before a leap would predict the next top of the spiral.
Lorenz Map... How is a simple curve there?
How is chaos different than randomness.
If this system were random, than there would be a cloud of fuzz.
Probability theory... In a random system, whatever can happen, can happen next with some probability.
You would not see just one outcome you would see a whole scatter or buckshot of outcomes.
In a deterministic system in contrast to a random system, only ONE thing can happen next.
One one thing can happen next given.
A strob light flashes
Record value Z, integrate the differential equation until the next peak and then ZAP the light goes off.
And keep repeating. Strob light triggered when a maximum is reached.
Lorenz map on only works for a system when it is on its attractor.
But remember there are transient times that it takes for the system to reach the attractor.
Transient behavior is just an artifact of how we started it. Let that garbage sort itself out until on attractor.
Why is the Lorenz map so important? Becaue it is so simple.
Simply
Tell me a Zn, tell me the next Zn+1
Iterated map lightning fast and captures the heart of
Great boiling down of information in the differential equations (much less cumbersome).
The true laws of physics and chemistry and the laws of nature are expressed in differential equations.
Leave differential equations behind..
Exploration of iterated maps provide some of the biggest insights in Chaos.
Lessons So Far
Lesson #1 - Chaos is not the opposite of order; it's a mix of order and randomness in the folowing senses.
Chaos is unpredictable and random looking
- in the long run because of the butterfly effect
Chaos is predictable and orderly
- in the short run because it obeys deterministic laws
- in the long run because of a kind of order persists as embodied by the strange attractor (overall predictability by being confined to the strange attractor).
- in the medium term, using iterated maps there is great structure there too.
Medium term dynamics are ordered and structured too... Not the very shortest term dynamics governed by the differential equation
ALL THESE STRUCTURES SHOW ORDER IN CHAOS
Lesson #2 - Order in Chaos is due to nonlinear relationships.
Nonlinear relationships...
Nonlinear: Causes can produce disproportionate effects, unlike a linear system.
Linear ....has something to do with lines... Lorenz maps is NOT a line, its a witches hat.
Nonlinearity is the most important idea in the entire course. The Mysteries of Non-linearity.
Lorenzs discoveries fell like the tree in the forest.
Lorenz discovered butterfly effect, the strange attractor, the iterated map, he's got computers, you would think people would get it... But people did not get it? Why?
60's was very specialized, not a lot of talking out
Journal of Atmospheric sciences... Lorenz was a meterologists.
Chaos is unpredictable and random looking
- in the long run because of the butterfly effect
Chaos is predictable and orderly
- in the short run because it obeys deterministic laws
- in the long run because of a kind of order persists as embodied by the strange attractor (overall predictability by being confined to the strange attractor).
- in the medium term, using iterated maps there is great structure there too.
Medium term dynamics are ordered and structured too... Not the very shortest term dynamics governed by the differential equation
ALL THESE STRUCTURES SHOW ORDER IN CHAOS
Lesson #2 - Order in Chaos is due to nonlinear relationships.
Nonlinear relationships...
Nonlinear: Causes can produce disproportionate effects, unlike a linear system.
Linear ....has something to do with lines... Lorenz maps is NOT a line, its a witches hat.
Nonlinearity is the most important idea in the entire course. The Mysteries of Non-linearity.
Lorenzs discoveries fell like the tree in the forest.
Lorenz discovered butterfly effect, the strange attractor, the iterated map, he's got computers, you would think people would get it... But people did not get it? Why?
60's was very specialized, not a lot of talking out
Journal of Atmospheric sciences... Lorenz was a meterologists.